Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

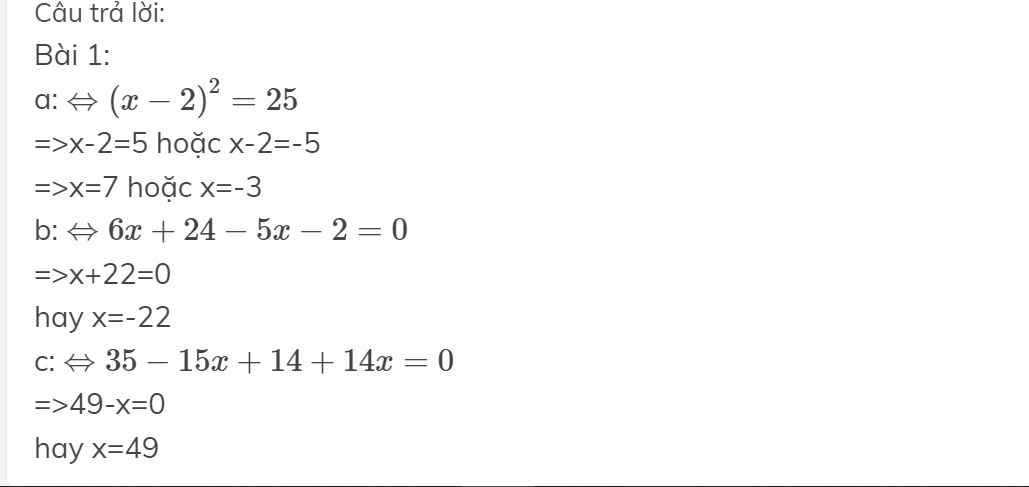
Bài 2:
a: \(=xy+xz-xy+yz\)
\(=xz+yz=z\left(x+y\right)\)
b: \(=x\left(y-z-y-a\right)\)
\(=x\left(-z-a\right)=-x\left(z+a\right)\)



Tìm các số nguyên x, y, z đồng thời thoả mãn các điều kiện sau :
x2 = y - 1 ; y2 = z -1 ; z2 = x - 1

Lời giải:
Ta có: \(\left\{\begin{matrix} x^2=y-1\\ y^2=z-1\\ z^2=x-1\end{matrix}\right.\)\(\Rightarrow \left\{\begin{matrix} x^2-y^2=y-z\\ y^2-z^2=z-x\\ z^2-x^2=x-y\end{matrix}\right.\)
\(\Rightarrow (x^2-y^2)(y^2-z^2)(z^2-x^2)=(x-y)(y-z)(z-x)\)
\(\Leftrightarrow (x-y)(y-z)(z-x)[(x+y)(y+z)(z+x)-1]=0\)
Giả sử 2 trong 3 số \(x,y,z\) bằng nhau \((x=y)\)
Thay vào PT 1: \(x^2=y-1=x-1\Leftrightarrow x^2-x+1=0\)
\(\Leftrightarrow (x-\frac{1}{2})^2+\frac{3}{4}=0\) (vô lý)
Do đó \(x\neq y\neq z\)
\(\Leftrightarrow (x-y)(y-z)(z-x)\neq 0\)
Suy ra \((x+y)(y+z)(z+x)=1\) (1)
Vì \(x,y,z\in\mathbb{Z}\Rightarrow x+y,y+z,z+x\in\mathbb{Z}\) (2)
Từ (1),(2) suy ra \(x+y,y+z,z+x\in \left\{-1;1\right\}\)
Vì chỉ có 2 giá trị mà có 3 số nên tồn tại 2 số có cùng giá trị 1 hoặc -1
Giả sử \(x+y=y+z\Rightarrow x=z\) (vô lý vì \(x\neq y\neq z\) )
Vậy không tồn tại bộ 3 số nguyên x,y,z thỏa mãn.
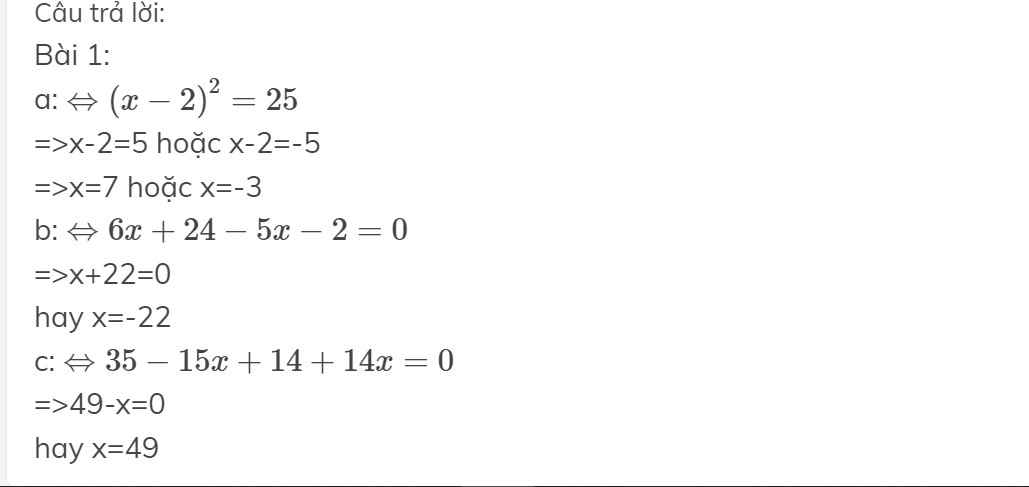

\(1-\frac{1}{2}+1+1.2\)
\(=\frac{1}{2}+1+2\)
\(=\frac{1}{2}+3=3\frac{1}{2}\)