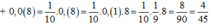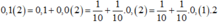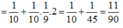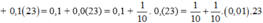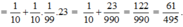NB
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ES
0
NK
29 tháng 8 2019
Kéo dài OB cắt đường thẳng a tại D. Tính được ^OAD rồi suy ra ^AOB
5 tháng 10 2019
máy tính xin hân hạnh đồng hành cùng với lê Kiều Trinh
VP
1
DD
Đoàn Đức Hà
Giáo viên
6 tháng 7 2021
Ta có: \(\widehat{B_1}+\widehat{B_2}=180^o\)(hai góc kề bù)
suy ra \(\widehat{B_2}+\frac{1}{2}\widehat{B_2}=\frac{3}{2}\widehat{B_2}=180^o\Leftrightarrow\widehat{B_2}=120^o\)
\(\widehat{B_1}=\frac{1}{2}\widehat{B_2}=120^o\div2=60^o\)
Có \(a//b\)nên \(\widehat{B_1}=\widehat{A_1}\)(hai góc so le trong)
suy ra \(\widehat{A_1}=60^o\)
N
3
29 tháng 10 2016
Bài 1:
\(0,0\left(8\right)=\frac{1}{10}\cdot0,\left(8\right)=\frac{1}{10}\cdot0,\left(1\right)\cdot8=\frac{4}{5}\cdot\frac{1}{9}=\frac{4}{45}\)
\(0,1\left(2\right)=0,1+0,0\left(2\right)=\frac{1}{10}+\frac{1}{10}\cdot0,\left(2\right)=\frac{1}{10}+\frac{1}{10}\cdot0,\left(1\right)\cdot2=\frac{1}{10}+\frac{1}{5}\cdot\frac{1}{9}=\frac{1}{10}+\frac{1}{45}=\frac{11}{90}\)
\(0,1\left(23\right)=0,1+0,\left(23\right)=\frac{1}{10}+0,\left(01\right)\cdot23=\frac{1}{10}+\frac{1}{99}\cdot23=\frac{1}{10}+\frac{23}{99}=\frac{329}{990}\)