
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Hai mặt phẳng cắt nhau, vì 1: 2: (-1) ≠ 2: 3: (-7)
b) Hai mặt phẳng cắt nhau, vì: 1: (-2): 1 ≠ 2: (-1): 4
c) Hai mặt phẳng song song, vì: 1/2=1/2=1/2 ≠ -1/3
d) Hai mạt phẳng cắt nhau, vì: 3: (-2): 3 ≠ 9: (-6): (-9)
e) Hai mặt phẳng trung nhau, vì: 1/10=-1/(-10)=2/20=-4/(-40).
#rin

Phương trình đường thẳng SB: x - t, y = 2t, z = 2 - 2t. Để tìm B' ta giải hệ
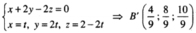
Tương tự, C'(0; 1; 1)

Đường thẳng qua B và vuông góc với (P) có phương trình:
x = 1 + t; y = 2 + 2t; z = -2t.
Để tìm giao điểm B 0 của đường thẳng này với (P) ta giả hệ
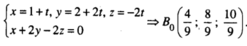
Từ đó suy ra điểm đối xứng với B qua (P) là 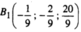

\(x.0,\left(2\right)+0,\left(3\right)=0,\left(77\right)\)
\(\Rightarrow x.\frac{2}{9}+\frac{3}{9}=\frac{7}{9}\)
\(\Rightarrow\frac{2x}{9}=\frac{7}{9}-\frac{3}{9}\)
\(\Rightarrow\frac{2x}{9}=\frac{4}{9}\)
\(\Rightarrow x=2\)
Vậy x = 2

M∈ (S) : (x0 - 2)2 + (y0-1)2 +(z0-1)2 =9.
A=x0+2y0+2z0=(x0-2)+2(y0-1)+2(z0-1)+6
Dùng BĐT bunhiacopski
[(x0-2)+2(y0-1)+2(z0-1)]2 ≤ (1+4+4).[(x0 - 2)2 + (y0-1)2 +(z0-1)2 ]
≤ 81
-9 ≤ (x0-2)+2(y0-1)+2(z0-1) ≤ 9.
-3 ≤ A ≤ 12. vậy GTNN của A = -3.
Dấu bằng xảy ra khi :
x0+2y0+2z0 = -3
và \(\dfrac{x0-2}{1}=\dfrac{y0-1}{1}=\dfrac{z0-1}{1}\)
Giải hệ được x0=1, y0=z0=-1. Suy ra: x0+y0+z0 = -1

Nhận xét : \(lg\tan1^0+lg\tan89^0=lg\left(\tan1^0.\tan89^0\right)=lg1=0\)
\(lg\tan2^0+lg\tan88^0=lg\left(\tan1^0.\tan88^0\right)=lg1=0\)
...................................................................................
....................................................................................
Và \(lg\tan45^0=lg1=0\)
Suy ra \(S=lg\tan1^0+lg\tan2^0+lg\tan3^0+......+lg\tan89^0\)
\(=\left(lg\tan1^0+lg\tan89^0\right)+\left(lg\tan2^0+lg\tan88^0\right)+....+lg\tan45^0\)
Vậy \(S=lg\tan1^0+lg\tan2^0+lg\tan3^0+...+lg\tan89^0=0\)

Điểm cực tiểu của hàm số y = -x3 + 3x +4 là
A. x = -1
B. x = 1
C. x = -3
=0
0