
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: Xét ΔMAB và ΔMCD có
MA=MC
\(\hat{AMB}=\hat{CMD}\) (hai góc đối đỉnh)
MB=MD
Do đó: ΔMAB=ΔMCD
=>AB=CD
ΔMAB=ΔMCD
=>\(\hat{MAB}=\hat{MCD}\)
=>\(\hat{MCD}=90^0\)
=>CD⊥CA
b: Xét ΔDCB có CB+CD>BD
mà CD=AB
nên CB+AB>BD
=>BA+BC>2BM
c: Ta có: ΔABC vuông tại A
=>BC là cạnh huyền
=>BC là cạnh lớn nhất trong ΔABC
=>BC>AB
mà AB=CD
nên BC>CD
Xét ΔCBD có CB>CD
ma \(\hat{CDB};\hat{CBD}\) lần lượt là góc đối diện của các cạnh CB,CD
nên \(\hat{CDB}>\hat{CBD}\)
mà \(\hat{CDB}=\hat{ABD}\) (ΔMAB=ΔMCD)
nên \(\hat{ABD}>\hat{CBD}\)
Bài 3:
a: Xét ΔAEB vuông tại E và ΔADC vuông tại D có
AB=AC
\(\hat{EAB}\) chung
Do đó: ΔAEB=ΔADC
=>AE=AD
=>ΔAED cân tại A
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
AD=AE
Do đó: ΔADH=ΔAEH
=>\(\hat{DAH}=\hat{EAH}\)
=>AH là phân giác của góc DAE
c: Xét ΔABC có \(\frac{AD}{AB}=\frac{AE}{AC}\)
nên DE//BC
d: Ta có: ΔADH=ΔAEH
=>HD=HE
ΔABE=ΔACD
=>BE=CD
Ta có: BE=BH+HE
CD+CH+HD
ma BE=CD va HE=HD
nên HB=HC
=>H nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,H,M thẳng hàng

1.1) a) \(\left|2x-5\right|=4\)
\(\Rightarrow\left[\begin{array}{l}2x-5=4\\ 2x-5=-4\end{array}\Rightarrow\left[\begin{array}{l}2x=9\\ 2x=1\end{array}\Rightarrow\left[\begin{array}{l}x=\frac92\\ x=\frac12\end{array}\right.\right.\right.\)
vậy \(x\in\left\lbrace\frac92;\frac12\right\rbrace\)
b)) \(\frac13-\left|\frac54-2x\right|=\frac14\)
\(\left|\frac54-2x\right|=\frac13-\frac14\)
\(\left|\frac54-2x\right|=\frac{1}{12}\)
\(\Rightarrow\left[\begin{array}{l}\frac54-2x=\frac{1}{12}\\ \frac54-2x=-\frac{1}{12}\end{array}\Rightarrow\left[\begin{array}{l}2x=\frac54-\frac{1}{12}\\ 2x=\frac54-\left(-\frac{1}{12}\right)\end{array}\right.\right.\)
\(\Rightarrow\left[\begin{array}{l}2x=\frac76\\ 2x=\frac43\end{array}\Rightarrow\left[\begin{array}{l}x=\frac{7}{12}\\ x=\frac23\end{array}\right.\right.\)
vậy \(x\in\left\lbrace\frac{7}{12};\frac23\right\rbrace\)
\(c.\frac12-\left|x+\frac15\right|=\frac13\)
\(\left|x+\frac15\right|=\frac12-\frac13\)
\(\left|x+\frac15\right|=\frac16\)
\(\Rightarrow\left[\begin{array}{l}x+\frac15=\frac16\\ x+\frac15=-\frac16\end{array}\Rightarrow\left[\begin{array}{l}x=\frac16-\frac15\\ x=-\frac16-\frac15\end{array}\right.\right.\Rightarrow\left[\begin{array}{l}x=-\frac{1}{30}\\ x=-\frac{11}{30}\end{array}\right.\)
vậy \(x\in\left\lbrace-\frac{1}{30};-\frac{11}{30}\right\rbrace\)
\(d.\frac34-\left|2x+1\right|=\frac78\)
\(\left|2x+1\right|=\frac34-\frac78\)
\(\left|2x+1\right|=-\frac18\)
\(\) ⇒ x thuộc rỗng
1.2) a) \(2\left|2x-3\right|=\frac12\)
\(\left|2x-3\right|=\frac12:2=\frac12\cdot\frac12=\frac14\)
\(\left[\begin{array}{l}2x-3=\frac14\\ 2x-3=-\frac14\end{array}\Rightarrow\left[\begin{array}{l}2x=\frac14+3\\ 2x=-\frac14+3\end{array}\right.\right.\)
\(\left[\begin{array}{l}2x=\frac{13}{4}\\ 2x=\frac{11}{4}\end{array}\Rightarrow\left[\begin{array}{l}x=\frac{13}{4}:2=\frac{13}{4}\cdot\frac12=\frac{13}{8}\\ x=\frac{11}{4}:2=\frac{11}{4}\cdot\frac12=\frac{11}{8}\end{array}\right.\right.\)
vậy: \(x\in\left\lbrace\frac{13}{8};\frac{11}{8}\right\rbrace\)
\(\frac{b)1}{3}-\left|\frac54-2x\right|=\frac14\)
\(\left|\frac54-2x\right|=\frac13-\frac14\)
\(\left|\frac54-2x\right|=\frac{1}{12}\)
\(\left[\begin{array}{l}\frac54-2x=\frac{1}{12}\\ \frac54-2x=-\frac{1}{12}\end{array}\Rightarrow\left[\begin{array}{l}2x=\frac54-\frac{1}{12}\\ 2x=\frac54-\left(-\frac{1}{12}\right)\end{array}\right.\right.\)
\(\left[\begin{array}{l}2x=\frac76\\ 2x=\frac43\end{array}\Rightarrow\left[\begin{array}{l}x=\frac76:2=\frac76\cdot\frac12=\frac{7}{12}\\ x=\frac43:2=\frac43\cdot\frac12=\frac23\end{array}\right.\right.\)
vậy \(x\in\left\lbrace\frac{7}{12};\frac23\right\rbrace\)
\(c.\left|x+\frac{4}{15}\right|-\left|-3,75\right|=-\left|-2,15\right|\)
\(\left|x+\frac{4}{15}\right|-3,75=-2,15\)
\(\left|x+\frac{4}{15}\right|=3,75-2,15\)
\(\left|x+\frac{4}{15}\right|=1,6\)
\(\left[\begin{array}{l}x+\frac{4}{15}=1,6\\ x+\frac{4}{15}=-1,6\end{array}\right.\Rightarrow\left[\begin{array}{l}x=1,6-\frac{4}{15}\\ x=-1,6-\frac{4}{15}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac43\\ x=-\frac{28}{15}\end{array}\right.\)
vậy \(x\in\left\lbrace\frac43;-\frac{28}{15}\right\rbrace\)
Bài 1.5:
a: Ta có: \(6,5-\frac94:\left|x+\frac13\right|=2\)
=>\(\frac94:\left|x+\frac13\right|=6,5-2=4,5=\frac92\)
=>\(\left|x+\frac13\right|=\frac94:\frac92=\frac24=\frac12\)
=>\(\left[\begin{array}{l}x+\frac13=\frac12\\ x+\frac13=-\frac12\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac12-\frac13=\frac16\\ x=-\frac12-\frac13=-\frac56\end{array}\right.\)
b: Ta có: \(\frac{11}{4}+\frac32:\left|4x-\frac15\right|=\frac72\)
=>\(\frac32:\left|4x-\frac15\right|=\frac72-\frac{11}{4}=\frac{14}{4}-\frac{11}{4}=\frac34\)
=>\(\left|4x-\frac15\right|=\frac32:\frac34=\frac42=2\)
=>\(\left[\begin{array}{l}4x-\frac15=2\\ 4x-\frac15=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}4x=2+\frac15=\frac{11}{5}\\ 4x=-2+\frac15=-\frac95\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{11}{20}\\ x=-\frac{9}{20}\end{array}\right.\)
c: Ta có: \(\frac{15}{4}-2,5:\left|\frac34x+\frac12\right|=3\)
=>\(2,5:\left|\frac34x+\frac12\right|=\frac{15}{4}-3=\frac34\)
=>\(\left|\frac34x+\frac12\right|=\frac52:\frac34=\frac52\cdot\frac43=\frac{20}{6}=\frac{10}{3}\)
=>\(\left[\begin{array}{l}\frac34x+\frac12=\frac{10}{3}\\ \frac34x+\frac12=-\frac{10}{3}\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac34x=\frac{10}{3}-\frac12=\frac{20}{6}-\frac36=\frac{17}{6}\\ \frac34x=-\frac{10}{3}-\frac12=-\frac{20}{6}-\frac36=-\frac{23}{6}\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{17}{6}:\frac34=\frac{17}{6}\cdot\frac43=\frac{68}{18}=\frac{34}{9}\\ x=-\frac{23}{6}:\frac34=-\frac{23}{6}\cdot\frac43=\frac{-92}{18}=-\frac{46}{9}\end{array}\right.\)
d: ta có: \(\frac{21}{5}+3:\left|\frac{x}{4}-\frac23\right|=6\)
=>\(3:\left|\frac{x}{4}-\frac23\right|=6-\frac{21}{5}=\frac{30}{5}-\frac{21}{5}=\frac95\)
=>\(\left|\frac{x}{4}-\frac23\right|=3:\frac95=3\cdot\frac59=\frac53\)
=>\(\left[\begin{array}{l}\frac{x}{4}-\frac23=\frac53\\ \frac{x}{4}-\frac23=-\frac53\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac{x}{4}=\frac53+\frac23=\frac73\\ \frac{x}{4}=-\frac53+\frac23=-\frac33=-1\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac73\cdot4=\frac{28}{3}\\ x=-1\cdot4=-4\end{array}\right.\)
Bai 1.4:
a: \(\left|x+\frac14\right|-\frac34=5\%\)
=>\(\left|x+\frac14\right|=5\%+\frac34=\frac{1}{20}+\frac{15}{20}=\frac{16}{20}=\frac45\)
=>\(\left[\begin{array}{l}x+\frac14=\frac45\\ x+\frac14=-\frac45\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac45-\frac14=\frac{16}{20}-\frac{5}{20}=\frac{11}{20}\\ x=-\frac45-\frac14=-\frac{16}{20}-\frac{5}{20}=-\frac{21}{20}\end{array}\right.\)
b: \(2-\left|\frac34x-\frac14\right|=\left|-\frac54\right|\)
=>\(2-\left|\frac34x-\frac14\right|=\frac54\)
=>\(\left|\frac34x-\frac14\right|=2-\frac54=\frac34\)
=>\(\left[\begin{array}{l}\frac34x-\frac14=\frac34\\ \frac34x-\frac14=-\frac34\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac34x=\frac34+\frac14=\frac44=1\\ \frac34x=-\frac34+\frac14=-\frac24=-\frac12\end{array}\right.\)
=>\(\left[\begin{array}{l}x=1:\frac34=\frac43\\ x=-\frac12:\frac34=-\frac12\cdot\frac43=-\frac46=-\frac23\end{array}\right.\)
c: \(\frac32+\frac45\left|x-\frac34\right|=\frac74\)
=>\(\frac45\left|x-\frac34\right|=\frac74-\frac32=\frac74-\frac64=\frac14\)
=>\(\left|x-\frac34\right|=\frac14:\frac45=\frac14\cdot\frac54=\frac{5}{16}\)
=>\(\left[\begin{array}{l}x-\frac34=\frac{5}{16}\\ x-\frac34=-\frac{5}{16}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{5}{16}+\frac34=\frac{5}{16}+\frac{12}{16}=\frac{17}{16}\\ x=-\frac{5}{16}+\frac34=-\frac{5}{16}+\frac{12}{16}=\frac{7}{16}\end{array}\right.\)
d: \(4,5-\frac34\left|\frac12x+\frac53\right|=\frac56\)
=>\(\frac34\left|\frac12x+\frac53\right|=4,5-\frac56=\frac92-\frac56=\frac{27}{6}-\frac56=\frac{22}{6}=\frac{11}{3}\)
=>\(\left|\frac12x+\frac53\right|=\frac{11}{3}:\frac34=\frac{11}{3}\cdot\frac43=\frac{44}{9}\)
=>\(\left[\begin{array}{l}\frac12x+\frac53=\frac{44}{9}\\ \frac12x+\frac53=-\frac{44}{9}\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac12x=\frac{44}{9}-\frac53=\frac{44}{9}-\frac{15}{9}=\frac{29}{9}\\ \frac12x=-\frac{44}{9}-\frac53=-\frac{44}{9}-\frac{15}{9}=-\frac{64}{9}\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{29}{9}:\frac12=\frac{29}{9}\cdot2=\frac{58}{9}\\ x=-\frac{64}{9}:\frac12=-\frac{64}{9}\cdot2=-\frac{128}{9}\end{array}\right.\)
Bài 1.3:
a: \(2\left|3x-1\right|+1=5\)
=>2|3x-1|=4
=>|3x-1|=2
=>\(\left[\begin{array}{l}3x-1=2\\ 3x-1=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}3x=3\\ 3x=-1\end{array}\right.\Rightarrow\left[\begin{array}{l}x=1\\ x=-\frac13\end{array}\right.\)
b: \(\left|\frac{x}{2}-1\right|=3\)
=>\(\left[\begin{array}{l}\frac{x}{2}-1=3\\ \frac{x}{2}-1=-3\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac{x}{2}=3+1=4\\ \frac{x}{2}=-3+1=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}x=8\\ x=-4\end{array}\right.\)
c: \(\left|-x+\frac25\right|+\frac12=3.5\)
=>\(\left|x-\frac25\right|=3.5-\frac12=\frac72-\frac12=\frac62=3\)
=>\(\left[\begin{array}{l}x-\frac25=3\\ x-\frac25=-3\end{array}\right.\Rightarrow\left[\begin{array}{l}x=3+\frac25=\frac{17}{5}\\ x=-3+\frac25=-\frac{15}{5}+\frac25=-\frac{13}{5}\end{array}\right.\)
d: \(\left|x-\frac13\right|=2\frac15\)
=>\(\left|x-\frac13\right|=\frac{11}{5}\)
=>\(\left[\begin{array}{l}x-\frac13=\frac{11}{5}\\ x-\frac13=-\frac{11}{5}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{11}{5}+\frac13=\frac{33}{15}+\frac{5}{15}=\frac{38}{15}\\ x=-\frac{11}{5}+\frac13=-\frac{33}{15}+\frac{5}{15}=-\frac{28}{15}\end{array}\right.\)
Bài 1.2:
a: \(2\left|2x-3\right|=\frac12\)
=>\(\left|2x-3\right|=\frac14\)
=>\(\left[\begin{array}{l}2x-3=\frac14\\ 2x-3=-\frac14\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=3+\frac14=\frac{13}{4}\\ 2x=3-\frac14=\frac{11}{4}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{13}{8}\\ x=\frac{11}{8}\end{array}\right.\)
b: \(7,5-3\left|5-2x\right|=-4.5\)
=>3|2x-5|=7,5+4,5=12
=>|2x-5|=4
=>\(\left[\begin{array}{l}2x-5=4\\ 2x-5=-4\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=9\\ 2x=1\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac92\\ x=\frac12\end{array}\right.\)
c: \(\left|x+\frac{4}{15}\right|-\left|-3,75\right|=-\left|-2.15\right|\)
=>\(\left|x+\frac{4}{15}\right|=-2,15+3,75=1,6=\frac85\)
=>\(\left[\begin{array}{l}x+\frac{4}{15}=\frac85\\ x+\frac{4}{15}=-\frac85\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac85-\frac{4}{15}=\frac{24}{15}-\frac{4}{15}=\frac{20}{15}=\frac43\\ x=-\frac85-\frac{4}{15}=-\frac{24}{15}-\frac{4}{15}=-\frac{28}{15}\end{array}\right.\)
Bài 1.1:
a: |2x-5|=4
=>

Kết luận của định lý ứng với hình vẽ là:
\(\hat{tOz}\) = 90\(^0\)

Bài 2:
a: \(A=\frac17+\frac{1}{7^2}+\cdots+\frac{1}{7^{100}}\)
=>\(7A=1+\frac17+\cdots+\frac{1}{7^{99}}\)
=>\(7A-A=1+\frac17+\cdots+\frac{1}{7^{99}}-\frac17-\frac{1}{7^2}-\cdots-\frac{1}{7^{100}}\)
=>\(6A=1-\frac{1}{7^{100}}=\frac{7^{100}-1}{7^{100}}\)
=>\(A=\frac{7^{100}-1}{6\cdot7^{100}}\)
b: \(B=\frac53+\frac{5}{3^2}+\frac{5}{3^3}+\cdots+\frac{5}{3^{20}}\)
=>\(3B=5+\frac53+\frac{5}{3^2}+\cdots+\frac{5}{3^{19}}\)
=>\(3B-B=5+\frac53+\frac{5}{3^2}+\cdots+\frac{5}{3^{19}}-\frac53-\frac{5}{3^2}-\cdots-\frac{5}{3^{20}}\)
=>\(2B=5-\frac{5}{3^{20}}=\frac{5\cdot3^{20}-5}{3^{20}}\)
=>\(B=\frac{5\cdot3^{20}-5}{2\cdot3^{20}}\)
c: \(C=-\frac13+\frac{1}{3^2}-\frac{1}{3^3}+\frac{1}{3^4}-\cdots+\frac{1}{3^{50}}\)
=>\(3C=-1+\frac13-\frac{1}{3^2}+\frac{1}{3^3}-\cdots+\frac{1}{3^{49}}\)
=>\(3C+C=-1+\frac13-\frac{1}{3^2}+\frac{1}{3^3}-\cdots+\frac{1}{3^{49}}-\frac13+\frac{1}{3^2}-\frac{1}{3^3}+\frac{1}{3^4}-\cdots+\frac{1}{3^{50}}\)
=>\(4C=-1+\frac{1}{3^{50}}=\frac{-3^{50}+1}{3^{50}}\)
=>\(C=\frac{-3^{50}+1}{4\cdot3^{50}}\)
d: \(D=\left(-\frac17\right)^0+\left(-\frac17\right)^1+\left(-\frac17\right)^2+\cdots+\left(-\frac17\right)^{2017}\)
=>\(D=1-\frac17+\frac{1}{7^2}-\frac{1}{7^3}+\cdots-\frac{1}{7^{2017}}\)
=>\(7D=7-1+\frac17-\frac{1}{7^2}+\cdots-\frac{1}{7^{2016}}\)
=>\(7D+D=7-1+\frac17-\frac{1}{7^2}+\cdots-\frac{1}{7^{2016}}+1-\frac17+\frac{1}{7^2}-\frac{1}{7^3}+\cdots-\frac{1}{7^{2017}}\)
=>\(8D=7-\frac{1}{7^{2017}}=\frac{7^{2018}-1}{7^{2017}}\)
=>\(D=\frac{7^{2018}-1}{8\cdot7^{2017}}\)
e: \(E=\frac12+\frac{1}{2^3}+\frac{1}{2^5}+\cdots+\frac{1}{2^{99}}\)
=>\(4E=2+\frac12+\frac{1}{2^3}+\cdots+\frac{1}{2^{97}}\)
=>\(4E-E=2+\frac12+\frac{1}{2^3}+\cdots+\frac{1}{2^{97}}-\frac12-\frac{1}{2^3}-\frac{1}{2^5}-\cdots-\frac{1}{2^{99}}\)
=>\(3E=2-\frac{1}{2^{99}}=\frac{2^{100}-1}{2^{99}}\)
=>\(E=\frac{2^{100}-1}{3\cdot2^{99}}\)
Bài 1:
a: \(A=2\cdot4+4\cdot6+6\cdot8+\cdots+98\cdot100\)
\(=4\left(1\cdot2+2\cdot3+3\cdot4+\cdots+49\cdot50\right)\)
\(=4\left\lbrack1\left(1+1\right)+2\left(2+1\right)+3\left(3+1\right)+\cdots+49\left(49+1\right)\right\rbrack\)
\(=4\left\lbrack\left(1^2+2^2+\cdots+49^2\right)+\left(1+2+3+\cdots+49\right)\right\rbrack\)
\(=4\cdot\left\lbrack\frac{49\left(49+1\right)\left(2\cdot49+1\right)}{6}+\frac{49\cdot50}{2}\right\rbrack=4\cdot\left\lbrack\frac{49\cdot50\cdot99}{6}+49\cdot25\right\rbrack\)
\(=4\cdot\left\lbrack49\cdot25\cdot33+49\cdot25\right\rbrack=4\cdot49\cdot25\cdot34=100\cdot49\cdot34\)
=166600
b: \(B=1\cdot99+2\cdot98+\cdots+97\cdot3+98\cdot2+99\cdot1\)
\(=2\cdot\left(1\cdot99+2\cdot98+\cdots+48\cdot52+49\cdot51\right)+50^2\)
\(=2\cdot\left\lbrack1\left(100-1\right)+2\left(100-2\right)+\cdots+48\left(100-48\right)+49\left(100-49\right)\right\rbrack+50^2\)
\(=2\left\lbrack100\left(1+2+\cdots+49\right)-\left(1^2+2^2+\cdots+49^2\right)\right\rbrack\) +2500
\(=2\cdot\left\lbrack100\cdot\frac{49\cdot50}{2}-\frac{49\cdot\left(49+1\right)\left(2\cdot49+1\right)}{6}\right\rbrack+2500\)
\(=2\cdot\left\lbrack100\cdot49\cdot25-\frac{49\cdot50\cdot99}{6}\right\rbrack+2500\)
\(=2\cdot\left\lbrack100\cdot49\cdot25-49\cdot25\cdot33\right\rbrack+2500=2\cdot25\cdot49\left(100-33\right)+2500\)
\(=50\cdot49\cdot67+2500=166650\)
d: \(D=2^2+4^2+\cdots+98^2+100^2\)
\(=2^2\left(1^2+2^2+\cdots+49^2+50^2\right)\)
\(=4\cdot\frac{50\cdot\left(50+1\right)\left(2\cdot50+1\right)}{6}=4\cdot\frac{50\cdot51\cdot101}{6}\)
\(=4\cdot25\cdot17\cdot101=100\cdot17\cdot101=171700\)
e: \(E=1^2+3^2+5^2+\cdots+99^2\)
\(=\left(1^2+2^2+3^2+4^2+\cdots+99^2+100^2\right)-\left(2^2+4^2+\cdots+100^2\right)\)
\(=\frac{100\left(100+1\right)\left(2\cdot100+1\right)}{6}-2^2\left(1^2+2^2+\cdots+50^2\right)\)
\(=\frac{100\cdot101\cdot201}{6}-4\cdot\frac{50\left(50+1\right)\left(2\cdot50+1\right)}{6}\)
\(=50\cdot101\cdot67-4\cdot\frac{50\cdot51\cdot101}{6}\)
\(=50\cdot101\cdot67-4\cdot25\cdot17\cdot101=101\cdot50\left(67-2\cdot17\right)\)
\(=50\cdot101\cdot33=166650\)
f: \(F=1^2-2^2+3^2-4^2+\cdots+99^2-100^2\)
\(=\left(1-2\right)\left(1+2\right)+\left(3-4\right)\left(3+4\right)+\cdots+\left(99-100\right)\left(99+100\right)\)
=-(1+2+3+4+...+99+100)
\(=-100\cdot\frac{101}{2}=-50\cdot101=-5050\)

\(\frac{x}{10}=\frac{y}{5}\)
=>\(\frac{x}{2}=\frac{y}{1}\)
=>\(\frac{x}{4}=\frac{y}{2}\)
mà \(\frac{y}{2}=\frac{z}{3}\)
nên \(\frac{x}{4}=\frac{y}{2}=\frac{z}{3}\)
mà 2x-3y+4z=350
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{x}{4}=\frac{y}{2}=\frac{z}{3}=\frac{2x-3y+4z}{2\cdot4-3\cdot2+4\cdot3}=\frac{350}{14}=25\)
=>\(\begin{cases}x=25\cdot4=100\\ y=25\cdot2=50\\ z=25\cdot3=75\end{cases}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{a+b-c}{c}=\frac{a+c-b}{b}=\frac{b+c-a}{a}=\frac{a+b-c+a+c-b+b+c-a}{a+b+c}=\frac{a+b+c}{a+b+c}=1\)
=>\(\begin{cases}a+b-c=c\\ a+c-b=b\\ b+c-a=a\end{cases}\Rightarrow\begin{cases}a+b=2c\\ a+c=2b\\ b+c=2a\end{cases}\)
\(A=\frac{\left(a+b\right)\left(b+c\right)\left(a+c\right)}{abc}=\frac{2a\cdot2b\cdot2c}{abc}=8\)

Bài 8:
Chu vi đáy là:
3,5+3,5+3+6=7+9=16(cm)
Diện tích xung quanh là: \(16\cdot11,5=184\left(\operatorname{cm}^2\right)\)
Bài 9:
Diện tích đáy là:
\(S=\frac12\cdot7\cdot24=12\cdot7=84\left(m^2\right)\)
Thể tích của khối bê tông là:
\(84\cdot22=1848\left(m^3\right)\)
Số tiền phải trả là:
\(1848\cdot2500000=4620000000\) (đồng)
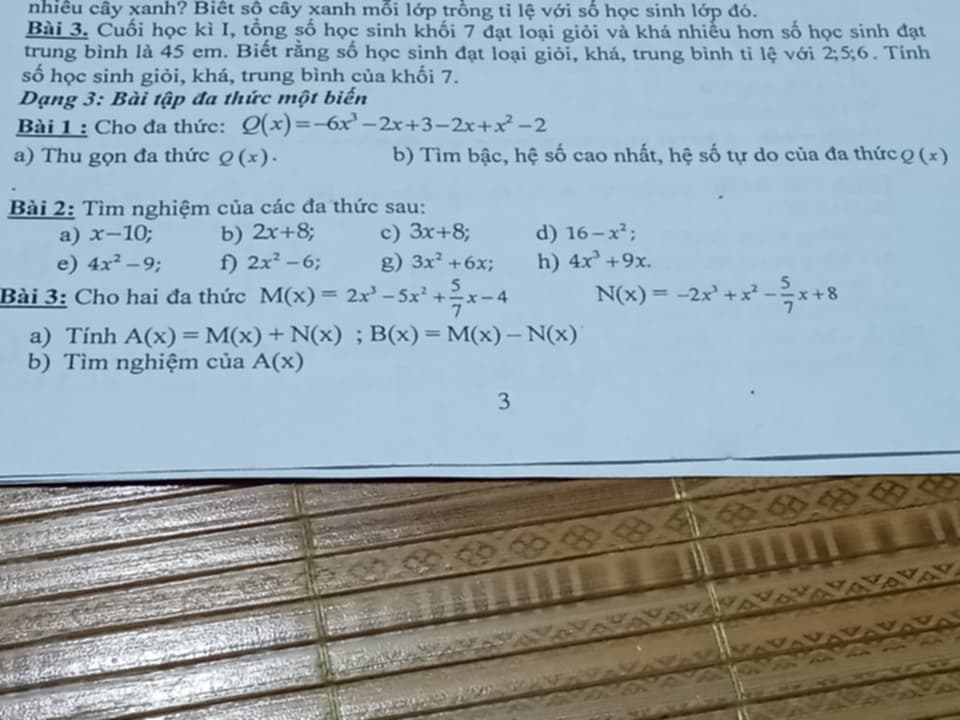







dễ