
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


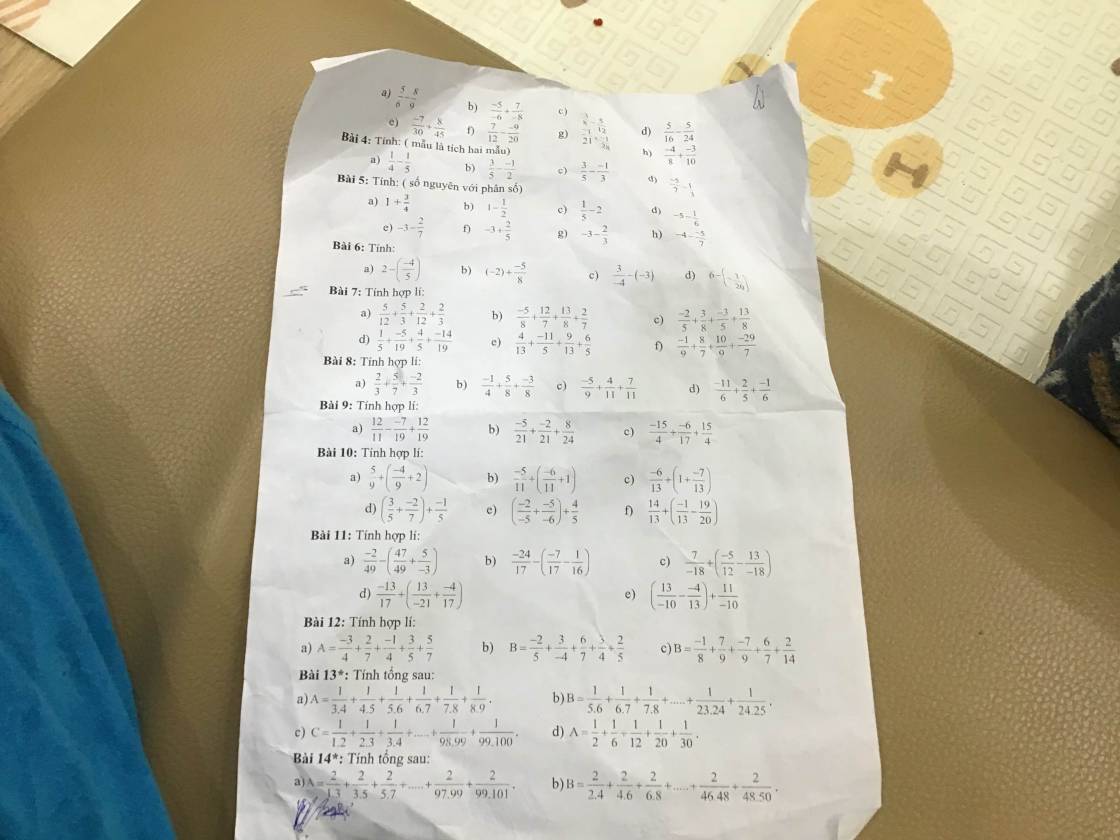
Bài 4:
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)

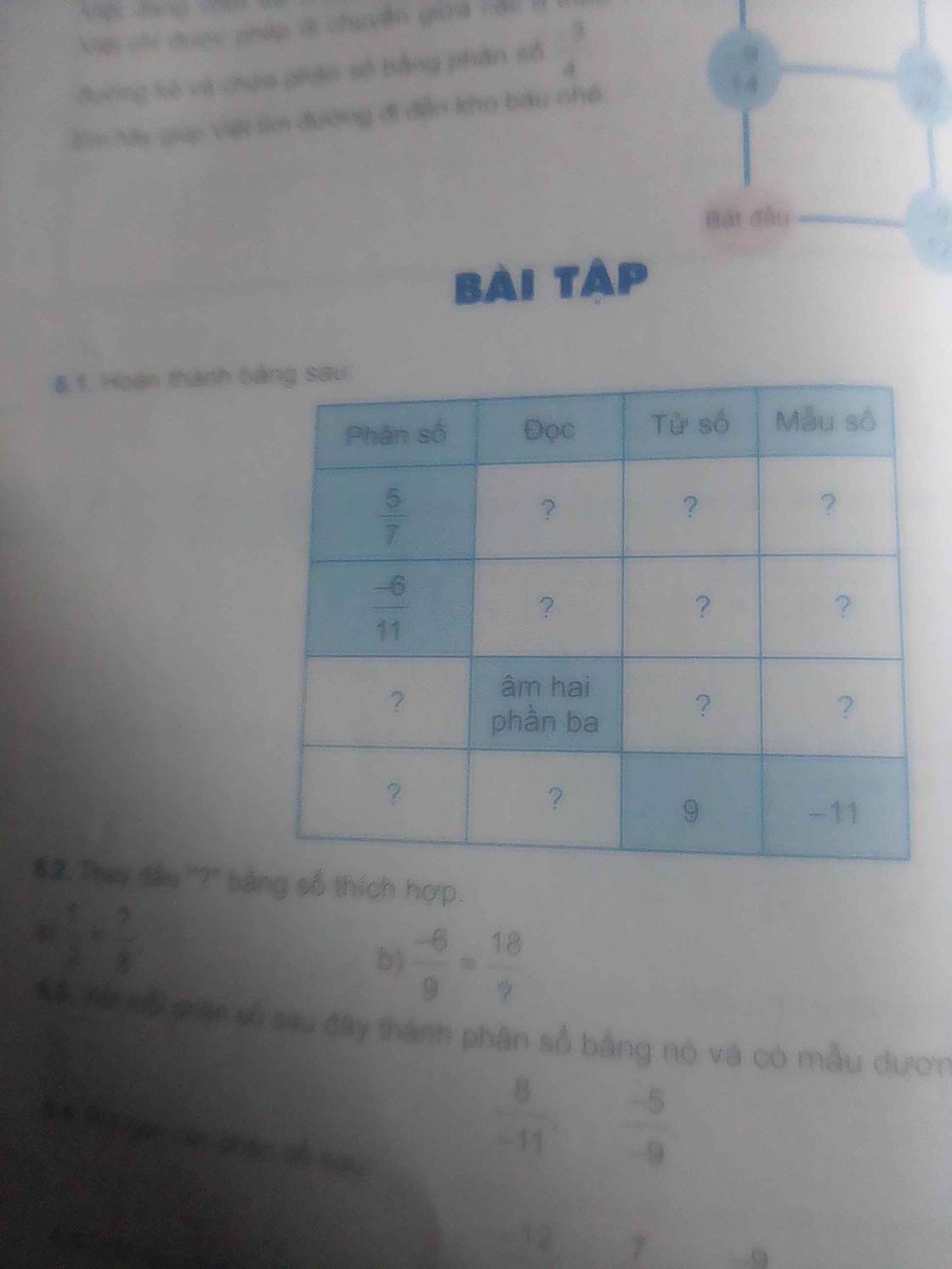
| Phân số | Đọc | Tử Số | Mẫu số |
| \(\dfrac{5}{7}\) | Năm phần bẩy | 5 | 7 |
| \(\dfrac{-6}{11}\) | âm sáu phần mười một | -6 | 11 |
| \(\dfrac{-2}{13}\) | âm hai phần ba | -2 | 13 |
| \(\dfrac{9}{-11}\) | chín phần âm mười một | 9 | -11 |

Bài 4:
\(a,\dfrac{-12}{16}=\dfrac{-12:4}{16:4}=\dfrac{-3}{4};\\ \dfrac{6}{-8}=\dfrac{6:\left(-2\right)}{-8:\left(-2\right)}=\dfrac{-3}{4}\\ Vì:-\dfrac{3}{4}=-\dfrac{3}{4}.Nên:\dfrac{-12}{16}=\dfrac{6}{-8}\\ ---\\ b,.\dfrac{33}{88}=\dfrac{33:11}{88:11}=\dfrac{3}{8}>0;\dfrac{-17}{76}< 0.Nên:-\dfrac{17}{76}< 0< \dfrac{33}{88}.Vậy:\dfrac{-17}{76}\ne\dfrac{33}{88}\)
Mỗi giờ máy bơm thứ nhất bơm vào 1/3 thể tích bể, đồng thời mỗi giờ máy bơm thứ hai hút ra được 1/5 thể tích bể:
Ta có: 1/3 - 1/5 = 5/15 - 3/15 = 2/15 (thể tích bể)
Vậy nếu dùng 2 máy bơm để cùng cấp và thoát nước trong bể 1 giờ thì bể thêm được thể tích là 2/15 bể. Dùng phân số dương nhé!

Bài 2:
a) Có hai đường thẳng trong hình
b) Điểm O không thuộc đường thẳng nào
c) A thuộc đường thẳng c và không thuộc đường thẳng d
d) Các điểm thuộc đường thẳng d là S và B
Các điểm không thuộc đường thẳng d là A và O

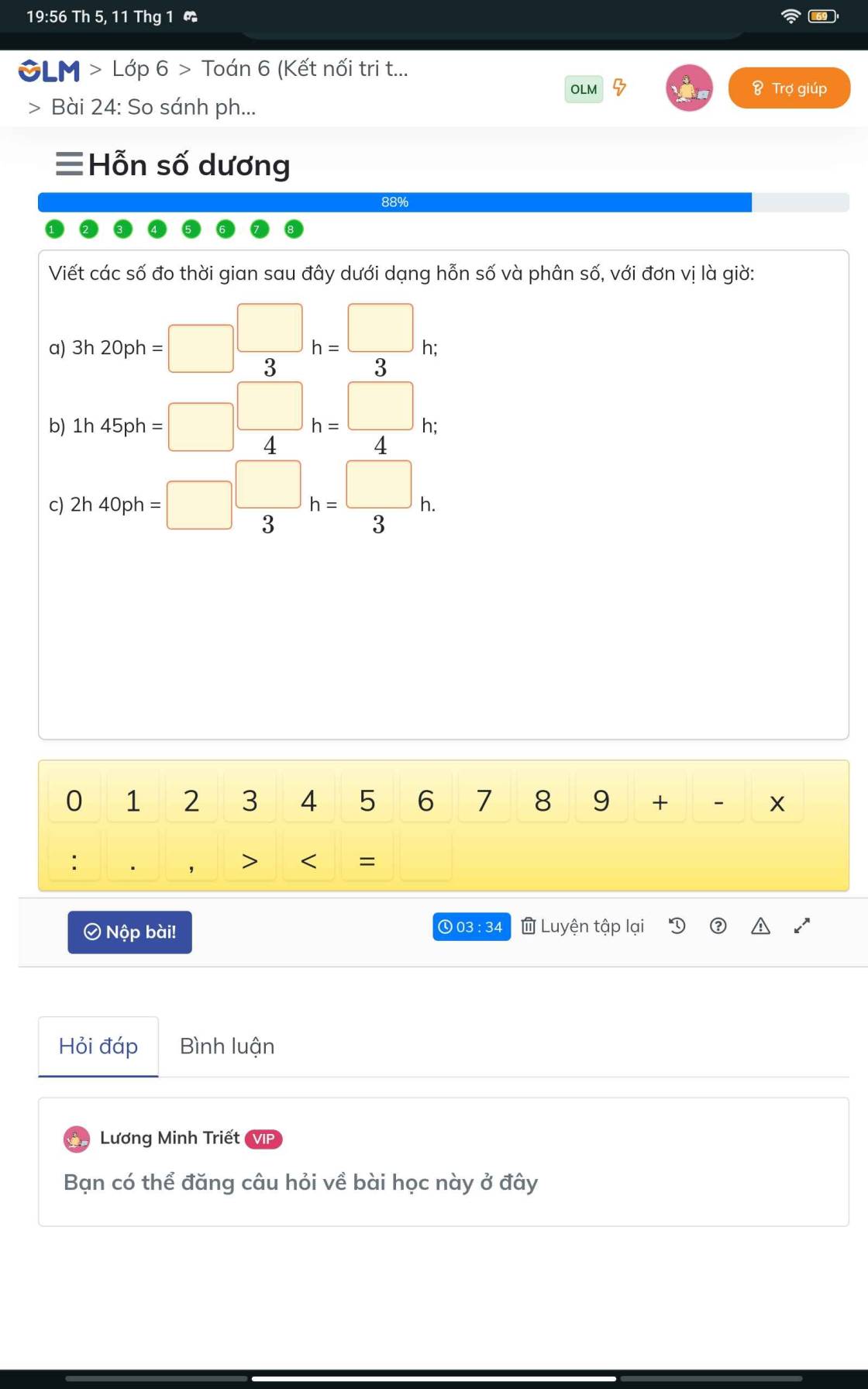
a) 3h 20ph = 3 và 1/3 = 10/3
b) 1h 45 ph = 1 và 3/4 = 7/4
c) 2h 40 ph = 2 và 2/3 = 8/3

\(a,-\dfrac{9}{4}< 0;\dfrac{1}{3}>0.Nên:-\dfrac{9}{4}< \dfrac{1}{3}\\ b,-\dfrac{8}{3}< -2;\dfrac{4}{-7}>-1.Nên:-\dfrac{8}{3}< -2< -1< \dfrac{4}{-7}\\ Vậy:-\dfrac{8}{3}< \dfrac{4}{-7}\\ c,\dfrac{9}{-5}< -1;\dfrac{7}{-10}>-1.Nên:\dfrac{9}{-5}< -1< \dfrac{7}{-10}.Vậy:\dfrac{9}{-5}< \dfrac{7}{-10}\\ d,\dfrac{3}{14}>0;-\dfrac{6}{14}< 0.Nên:\dfrac{3}{14}>0>-\dfrac{6}{14}.Vậy:\dfrac{3}{14}>-\dfrac{6}{14}\\ e,\dfrac{7}{-12}=\dfrac{7.3}{-12.3}=\dfrac{21}{-36};\dfrac{11}{-18}=\dfrac{11.2}{-18.2}=\dfrac{22}{-36}\\ Vì:\dfrac{21}{-36}>\dfrac{22}{-36}.Nên:\dfrac{7}{-12}>\dfrac{11}{-18}\)
\(f,-\dfrac{4}{7}< -\dfrac{1}{2};-\dfrac{4}{10}>\dfrac{-1}{2}.Nên:-\dfrac{4}{7}< -\dfrac{1}{2}< -\dfrac{4}{10}.Vậy:-\dfrac{4}{7}< -\dfrac{4}{10}\\ g,-\dfrac{8}{15}< -\dfrac{1}{2};\dfrac{5}{-24}>-\dfrac{1}{2}.Nên:-\dfrac{8}{15}< -\dfrac{1}{2}< \dfrac{5}{-24}.Vậy:-\dfrac{8}{15}< \dfrac{5}{-24}\\ h,\dfrac{69}{-230}=\dfrac{69:23}{-230:23}=\dfrac{3}{-10};\dfrac{-39}{143}=\dfrac{-39:13}{143:13}=\dfrac{-3}{11}\\ Vì:\dfrac{-3}{10}< -\dfrac{3}{11}.Vậy:\dfrac{69}{-230}< \dfrac{-39}{143}\\ i,\dfrac{7}{41}=1-\dfrac{34}{41};\dfrac{13}{47}=1-\dfrac{34}{47}\\ Vì:\dfrac{34}{41}>\dfrac{34}{47}.Nên:1-\dfrac{34}{41}< 1-\dfrac{34}{47}.Vậy:\dfrac{7}{41}< \dfrac{13}{47}\)

Các phân số trên đều có dạng: \(\dfrac{k}{k+n+2}\)
Chúng tối giản khi \(k\) và \(k+n+2\) nguyên tố cùng nhau
\(\Rightarrow k\) và \(k+n+2-k\) nguyên tố cùng nhau
\(\Rightarrow k\) và \(n+2\) nguyên tố cùng nhau
\(\Rightarrow n+2\) nguyên tố cùng nhau với 1;2;3;...;2002
Mà n nhỏ nhất \(\Rightarrow n+2=2003\) (do 2003 là số nguyên tố nên nó nguyên tố cùng nhau với mọi số nguyên)
\(\Rightarrow n=2001\)

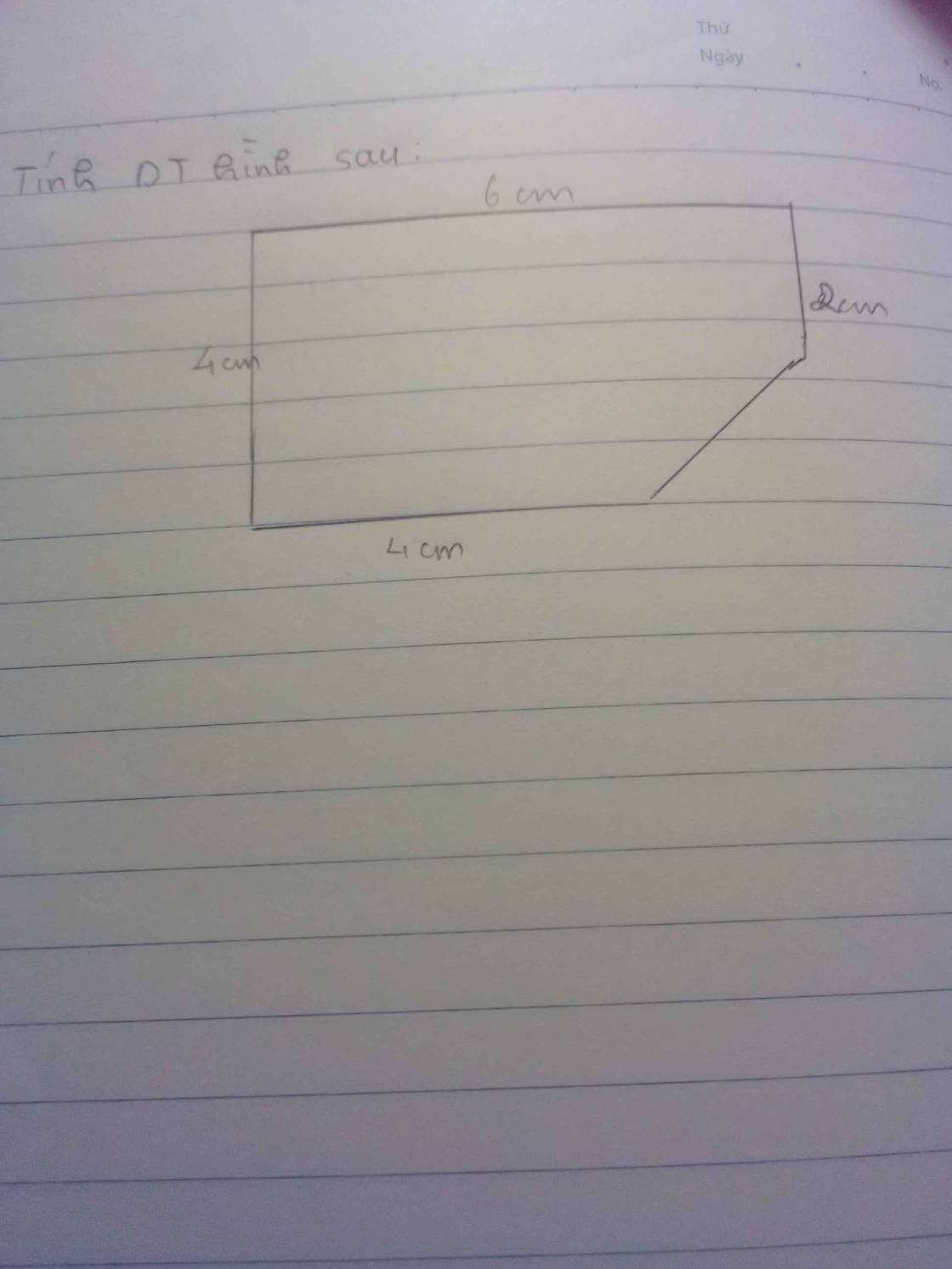
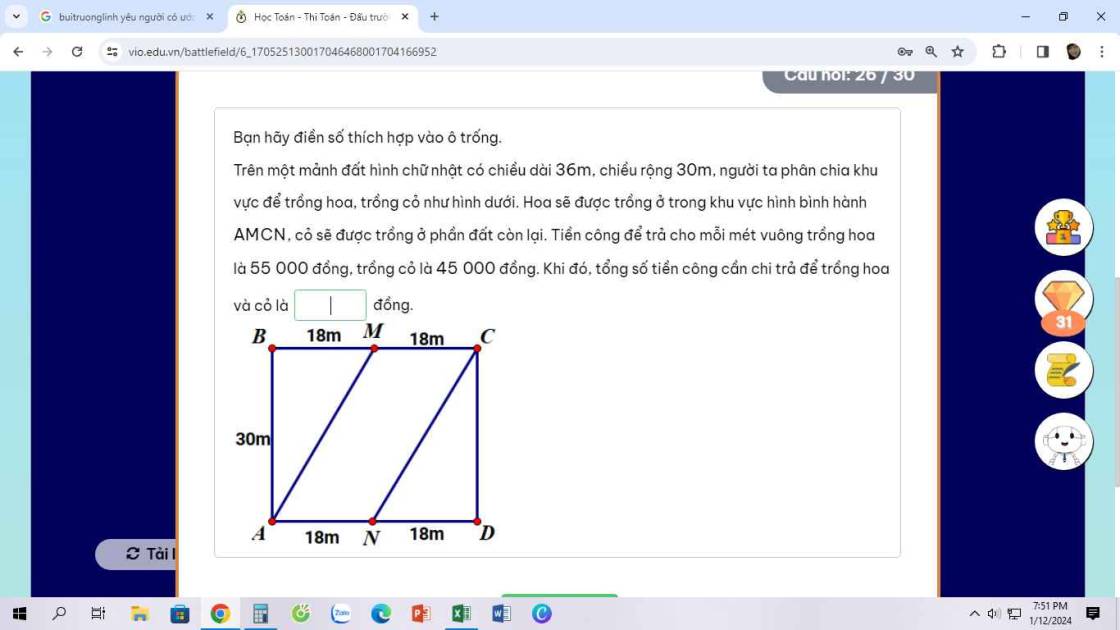
Diện tích mảnh đất là:
\(30\times\left(18+18\right)=1080\left(m^2\right)\)
Diện tích trồng hoa là:
\(30\times18=540\left(m^2\right)\)
Diện tích trồng cỏ là:
\(1080-540=540\left(m^2\right)\)
Tổng tiền cần chi trả là:
\(55000\times540+45000\times540=54000000\) (đồng)
Giải
Diện tích mảnh đất là:
30x(18+18)=1080(m vuông)
Diện tích trồng hoa là:
30x18=540(m vuông)
Diện tích trồng cỏ là:1080-540=540(m vuông)
Tổng số tiền cần chị trả là:
55000x540+45000x540=54000000(đồng)
Chúc bạn học tốt!



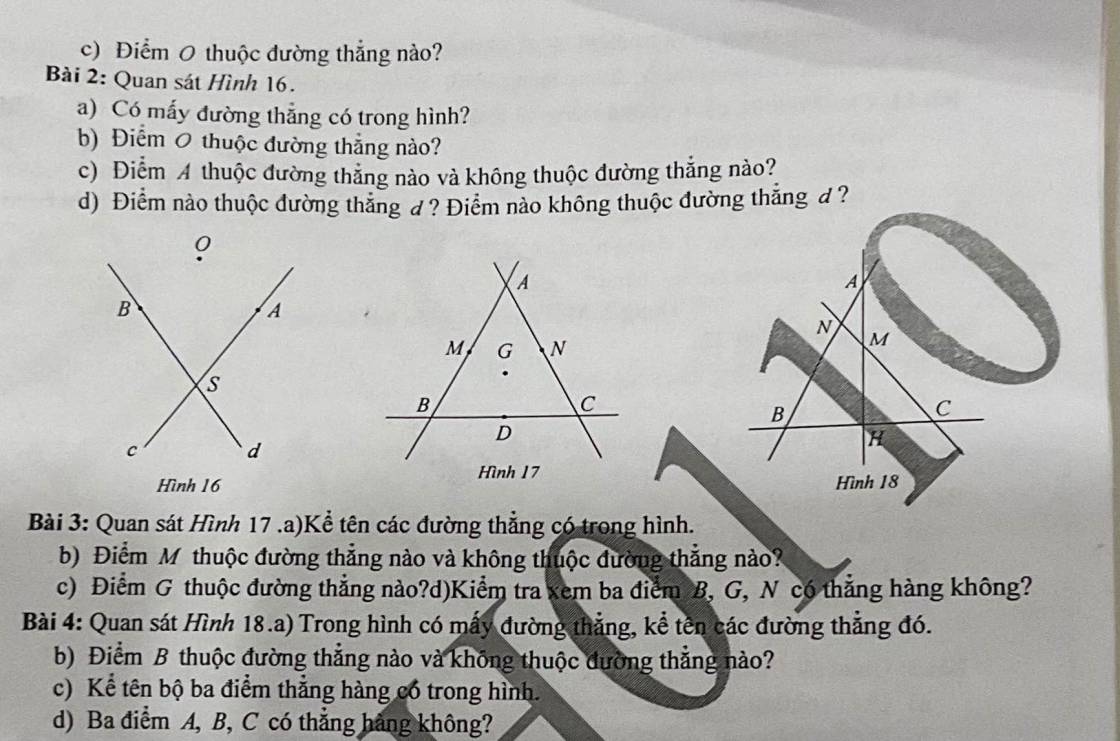
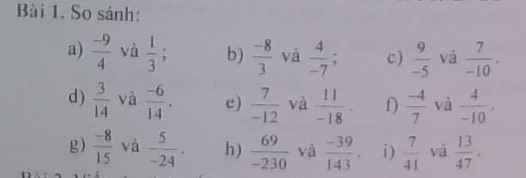
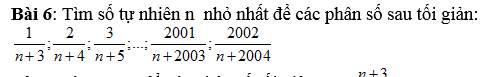
Đây là dạng toán nâng cao chuyên đề vòi nước. Cấu trúc thi chuyên thi học sinh giỏi các cấp. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Gấp rưỡi là gấp \(\dfrac{3}{2}\), vậy lượng nước nóng bằng \(\dfrac{3}{2}\) lượng nước lạnh khi bể đầy.
Khi bể đầy lượng nước nóng bằng: 3 : (3 + 2) = \(\dfrac{3}{5}\) (bể)
Khi bể đầy lượng nước lạnh bằng: 1 - \(\dfrac{3}{5}\) = \(\dfrac{2}{5}\) (bể)
Cứ một phút vòi lạnh chảy được: 1 : 17 = \(\dfrac{1}{17}\) (bể)
Thời gian vòi nước lạnh chảy được \(\dfrac{2}{5}\) bể là: \(\dfrac{2}{5}\) : \(\dfrac{1}{17}\) = 6,8 (phút)
Cứ một phút vòi nóng chảy được: 1 : \(23\) = \(\dfrac{1}{23}\) (bể)
Thời gian vòi nước nóng chảy được \(\dfrac{3}{5}\) bể là: \(\dfrac{3}{5}\) : \(\dfrac{1}{23}\) = 13,8 (phút)
Để khi bể đầy, lượng nước nóng gấp rưỡi lượng nước lạnh. Nếu mở vòi nước nóng trước thì cần mở vòi lạnh sau:
13,8 phút - 6,8 phút = 7 phút
Kết luận. Nếu mở vòi nước nóng trước thì cần mở vòi lạnh sau 7 phút, để khi bể đầy lượng nước nóng gấp rưỡi lượng nước lạnh.