Cho tam giác ABC có BC = 2 cm, góc A=105o , góc C=30o. Tính diện tích tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 7 2021
Kẻ đường cao AH
Trong tam giác vuông ABH:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{BC^2}{cotB+cotC}=\dfrac{1}{2}.\dfrac{6^2}{cot45^0+cot30^0}\approx11,4\left(cm^2\right)\)
21 tháng 10 2021
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)
HT
1
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Lời giải:
Theo định lý cos:
\(\cos C=\frac{a^2+b^2-c^2}{2ab}\Leftrightarrow \cos 30^0=\frac{12+4-c^2}{8\sqrt{3}}\)
\(\Rightarrow c^2=4\Rightarrow c=2\)
$c=b=2$ nên tam giác $ABC$ cân tại $A$
$\Rightarrow \widehat{A}=180^0-2.30^0=120^0$
$S_{ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}.2.2\sqrt{3}\sin 30^0=\sqrt{3}$ (đvdt)
3 tháng 9 2021
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan30^0\)
\(=2\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
CM
10 tháng 7 2019
Vẽ hình:
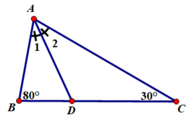
Áp dụng định lý góc ngoài trong các tam giác ABD và ACD ta có:
CM
23 tháng 6 2019
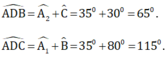
a) + Δ ABC vuông tại A, có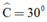 
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của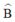 
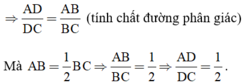
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
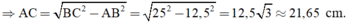
+ Chu vi tam giác ABC là:
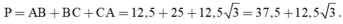
+ Diện tích tam giác ABC là:
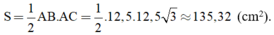
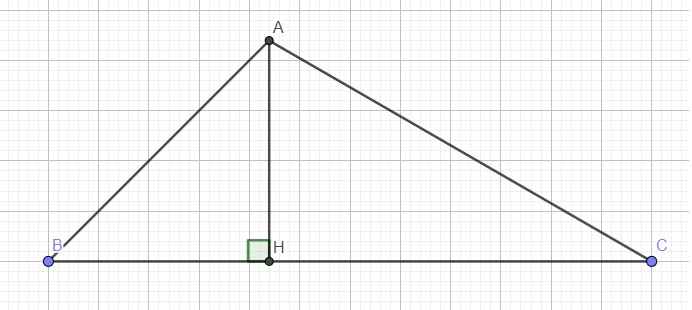
Ta có :
góc C = 180o - 105o - 30o = 45o
Kẻ đường cao AH
Gọi BH = x(cm) $\to$ CH = 2 - x(cm)
Trong tam giác AHB vuông tại H và tam giác AHC vuông tại H, ta có :
\(AH=BH.tanB=x.tan45^o=x\\ AH=CH.tanC=\left(2-x\right).tan30^o=\dfrac{\sqrt{3}}{3}\left(2-x\right)\)
Suy ra :
\(x=\dfrac{\sqrt{3}}{3}\left(2-x\right)\Leftrightarrow x=\dfrac{2\sqrt{3}}{3+\sqrt{3}}\)
Suy ra:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2\sqrt{3}}{3+\sqrt{3}}.2\simeq0,732\left(cm^2\right)\)