Đề kiểm tra học kì I (đề số 2)

Câu 1 (1đ):

Mẫu số liệu sau ghi lại cân nặng (đơn vị: ki-lô-gam) của các bạn tổ II lớp 10A lần lượt là:

$\,\,\,\,\,38\,\,\,\,\,40\,\,\,\,\,55\,\,\,\,\,44\,\,\,\,\,\,50\,\,\,\,\,82\,\,\,\,\,78\,\,\,\,\,65\,\,\,\,\,48\,\,\,\,\,44\,\,\,\,\,\,54$ .

Trung vị của mẫu số liệu trên là

50

.

49

.

48

.

54

.

Câu 2 (1đ):

Cho giá trị gần đúng của $\dfrac{23}{7}$ là $3,28$ . Sai số tuyệt đối của số $3,28$ xấp xỉ

\dfrac{0,06}{7}

.

0,04

.

\dfrac{0,04}{7}

.

0,06

.

Câu 3 (1đ):

Cho tam giác $ABC$ vuông tại $A$ , $G$ là trọng tâm tam giác $ABC,\, BC=a$ . Độ dài vectơ $\overrightarrow{AG}$ là

\dfrac{a}{6}

.

\dfrac{a}{3}

.

\dfrac{a\sqrt{3}}2

.

\dfrac{2a}{3}

.

Câu 4 (1đ):

Trên nửa đường tròn đơn vị, cho góc $\alpha$ như hình vẽ:

loading...

Các giá trị lượng giác của góc $\alpha$ là

\sin \alpha =1

;

\cos \alpha =0

;

\tan \alpha =0

;

\cot \alpha

không xác định.

\sin \alpha =0

;

\cos \alpha =1

;

\tan \alpha =1

;

\cot \alpha =0

.

\sin \alpha =1

;

\cos \alpha =0

;

\tan \alpha

không xác định;

\cot \alpha =0

.

\sin \alpha =1

;

\cos \alpha =0

;

\tan \alpha

không xác định;

\cot \alpha =1

.

Câu 5 (1đ):

Cho hàm số bậc hai $y=2x^2+bx+2 \, 023$ có đồ thị là parabol $(P)$ . Để $(P)$ có trục đối xứng là đường thẳng $x=4$ thì

b=-8

.

b=8

.

b=16

.

b=-16

.

Câu 6 (1đ):

Cho hàm số $y=f(x)$ xác định trên đoạn $[ -2;3 ]$ có đồ thị được cho như trong hình dưới đây:

$Cho hàm số $y=f(x)$ xác định trên đoạn $\left[ -2;3 \right]$ có đồ thị được cho như trong hình dưới đây$

Gọi $M$ , $m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của $f(x)$ trên đoạn $[ -2;3 ]$ . Tổng $M+m$ bằng

1

.

2

.

0

.

3

.

Câu 7 (1đ):

Cho hai tập hợp $A=\left[ -2;7 \right), \, B=\left(1;9 \right]$ . Tập $A\cup B$ là

\left[ -2;1 \right)

.

\left(1;7 \right)

.

\left(7;9 \right]

.

\left[ -2;9 \right]

.

Câu 8 (1đ):

Cho hai vectơ $\overrightarrow{a}$ ; $\overrightarrow{b}$ khác vectơ $\overrightarrow{0}$ thỏa mãn $\overrightarrow{a}.\overrightarrow{b}=\dfrac12\left| -\overrightarrow{a} \right|.\left| \overrightarrow{b} \right|$ . Khi đó góc giữa hai vectơ $\overrightarrow{a}$ ; $\overrightarrow{b}$ bằng

150^\circ

.

120^\circ

.

60^\circ

.

30^\circ

.

Câu 9 (1đ):

Cho tam giác $ABC$ và $M$ thỏa mãn $\overrightarrow{BM}=-3\overrightarrow{MC}$ . Mệnh đề nào sau đây đúng?

\overrightarrow{AM}=-\dfrac12\overrightarrow{AB}+\dfrac32\overrightarrow{AC}

\overrightarrow{AM}=\dfrac34\overrightarrow{AB}+\dfrac14\overrightarrow{AC}.

\overrightarrow{AM}=\dfrac14\overrightarrow{AB}+\dfrac34\overrightarrow{AC}.

\overrightarrow{AM}=\dfrac14\overrightarrow{AB}-\dfrac34\overrightarrow{AC}.

Câu 10 (1đ):

Cho biết $\cos \alpha =-\dfrac23.$ Giá trị của $P=\dfrac{\cot \alpha +3\tan \alpha }{2\cot \alpha +\tan \alpha }$ bằng

-\dfrac{19}{13}.

\dfrac{25}{13}.

\dfrac{19}{13}.

-\dfrac{25}{13}.

Câu 11 (1đ):

Giá trị lớn nhất của hàm số $y=\dfrac{2}{{{x}^{2}}-5x+9}$ bằng

\dfrac{4}{11}

.

\dfrac{11}{4}

.

\dfrac{11}{8}

.

\dfrac{8}{11}

.

Câu 12 (1đ):

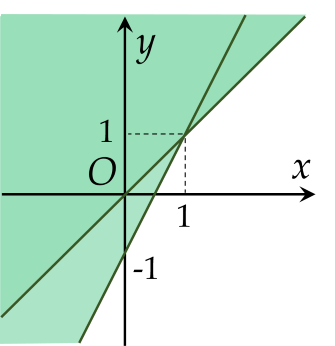
Miền nghiệm (phần không tô màu) trong hình vẽ biểu diễn tập nghiệm của hệ bất phương trình nào dưới đây?

loading...

\left\{ \begin{aligned} & 2x+y>0 \\ & x-2y-1>0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+4y>0 \\ & x-y-2<0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & 4x+y<0 \\ & x-y-2>0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & 4x+y<0 \\ & x-y-2<0 \\ \end{aligned} \right.

.

Câu 13 (1đ):

Cuối học kì I vừa qua, bạn An đạt được kết quả sáu môn như sau:

Môn	Điểm trung bình
Toán	$7,2$
Văn	$8,0$
Anh	$5,8$
Lý	$7,2$
Hóa	$9,0$
Sinh	$4,6$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Điểm trung bình các môn thi học kì của bạn An làm tròn đến hàng phần mười là $7,0$ .
b) Điểm trung bình các môn thi học kì của bạn An là $7,3$ .
c) Khoảng biến thiên của bảng điểm của bạn An bằng $3,4$ .
d) Khoảng tứ phân vị bảng điểm của bạn An bằng $2,2$ .

Câu 14 (1đ):

Cho tam giác $ABC$ có trực tâm $H$ và $M$ là trung điểm $BC$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{HA}.\overrightarrow{CB}=1$ .
b) $\overrightarrow{BH}.\overrightarrow{CA}=0$ .
c) $\overrightarrow{MH}.\overrightarrow{MA}=\dfrac{BC^2}{4}$ .
d) $MH^2+MA^2=AH^2+\dfrac{BC^2}{2}$ .

Câu 15 (1đ):

Cho hàm số $y=\dfrac{m-2}{m+1}x+2m-1$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Với $m>2$ , hàm số đồng biến trên $\mathbb{R}$ .
b) Với $m\lt 1$ , hàm số nghịch biến trên $\mathbb{R}$ .
c) Có $2$ giá trị nguyên của tham số $m$ để hàm số đã cho nghịch biến trên $\mathbb{R}$ .
d) Có $4$ giá trị của tham số $m$ để giá trị lớn nhất của hàm số trên $[ -2;3 ]$ bằng $5$ .

Câu 16 (1đ):

Cho hàm số $y=-x^2+6x-5$ có đồ thị $(P)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $y>0$ khi $x\in (1;5)$ .
b) $y\lt 0$ khi $x\in (-\infty ;1)\cup (5;+\infty)$ .
c) Giá trị lớn nhất của hàm số bằng $3$ .
d) Đường thẳng $d: \, y=4x-m$ cắt đồ thị $(P)$ tại hai điểm phân biệt khi $m>4$ .

Câu 17 (1đ):

Trên biển Đông, một tàu chuyển động đều từ vị trí $A$ theo hướng N $20^\circ$ W với vận tốc $30$ km/h. Sau $5$ giờ, tàu đến được vị trí $B$ . $A$ cách $B$ bao nhiêu ki lô mét và về hướng S $20^\circ$ E so với $B$ ?

Trả lời:

Câu 18 (1đ):

Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày:

$\,\,\,\,\,7\,\,\,\,\,8\,\,\,\,\,22\,\,\,\,\,20\,\,\,\,\,15\,\,\,\,\,18\,\,\,\,\,19\,\,\,\,\,13\,\,\,\,\,11$

Khoảng tứ phân vị cho mẫu số liệu này bằng bao nhiêu?

Trả lời:

Câu 19 (1đ):

Giả sử chúng ta cần đo chiều cao $CD$ của một cái tháp với $C$ là chân tháp, $D$ là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm $A, \, B$ có khoảng cách $AB=30$ m sao cho ba điểm $A, \, B, \, C$ thẳng hàng, người ta đo được các góc $\widehat{CAD}=43^\circ$ , $\widehat{CBD}=67^\circ$ .

loading...

Tính chiều cao $CD$ của tháp (Làm tròn kết quả đến chữ số hàng đơn vị của mét)

Trả lời:

Câu 20 (1đ):

Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học tìm được quy luật rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có $n$ con cá thì trung bình mỗi con cá sau một vụ cân nặng $P(n)=360-10n$ (đơn vị khối lượng). Người nuôi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lượng cá sau mỗi vụ thu được là nhiều nhất?

Trả lời:

Câu 21 (1đ):

Có hai địa điểm $A,\,B$ cùng nằm trên một tuyến quốc lộ thẳng. Khoảng cách giữa $A$ và $B$ là $30,5$ km. Một xe máy xuất phát từ $A$ lúc $7$ giờ theo chiều từ $A$ đến $B$ . Lúc $9$ giờ, một ô tô xuất phát từ $B$ chuyển động thẳng đều với vận tốc $80$ km/h theo cùng chiều với xe máy. Chọn $A$ làm mốc, chọn thời điểm $7$ giờ làm mốc thời gian và chọn chiều từ $A$ đến $B$ làm chiều dương. Phương trình chuyển động của xe máy là $y=2t^2+36t$ , trong đó $y$ tính bằng ki-lô-mét, $t$ tính bằng giờ. Đến lúc ô tô đuổi kịp xe máy thì hai xe dừng lại, vị trí đó cách điểm $B$ bao nhiêu km?

Trả lời:

Câu 22 (1đ):

Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:

▪️ Mỗi kg sản phẩm loại I cần $2$ kg nguyên liệu và $30$ giờ, thu lời (lãi) được $40$ nghìn đồng.

▪️ Mỗi kg sản phẩm loại II cần $4$ kg nguyên liệu và $15$ giờ, thu lời được $30$ nghìn đồng.

Xưởng có $200$ kg nguyên liệu và $1 \, 200$ giờ làm việc tối đa. Để có mức tiền lãi cao nhất, xưởng cần sản xuất $a$ sản phẩm loại I và $b$ sản phẩm loại II. Tính $a + b$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP