Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng tính chất đường trung bình, ta chứng minh được DE//BC

Xét ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: DE//CB
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
bạn ơi bạn chứng minh sai rùi ở cuối ý nếu mà 2 góc đáy bằng nhau chưa chắc đã là hình thang cân đâu chẳng hạn hình vuông 2 đáy cũng = nhau ......
nên bạn cm sai rùi sửa lại đi bạn cm 2 đường chéo bằng nhau

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔEBC=ΔDCB
b: ΔEBC=ΔDCB
=>EB=DC
AE+EB=AB
AD+DC=AC
mà EB=DC và AB=AC
nên AE=AD
Xét ΔABC có AE/AB=AD/AC
nên ED//BC
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
Hình thang BEDC có \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân

a: Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
b: \(\widehat{EBC}=\widehat{DCB}=\dfrac{180^0-40^0}{2}=70^0\)
\(\widehat{BED}=\widehat{CDE}=180^0-70^0=110^0\)
Bạn tự vẽ hình
a) Có tg ABC cân tại A
=>góc ABC=góc ACB
có BD là trung tuyến => D là tđ
có CE là trung tuyến =>E là tđ
Xét tg ABC có
E là tđ AB
D là tđ AC
=> ED là đg tb
=> ED//BC
=> EDBC là hình thg
mà góc ABC= góc ACB(cmt)
=>EDBC là hình thg cân
b) góc A+góc B+ góc C=180
=>40+B+C+180
Mà B=C (cmt)
B=C= (180-40)/2
B=C=70 độ
B+D=90độ
=>D=20 độ
=> E=20 độ( EDBC cân)

Bạn vào
Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
a: Xét ΔADB và ΔAEC có
góc BAD chung
AB=AC
góc ABD=góc ACE
Do đó: ΔADB=ΔAEC
b: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà góc EBC=góc DCB
nên BEDC là hình thang cân
Xét ΔEDB có góc EDB=góc EBD(=góc DBC)
nên ΔEDB cân tại E
=>BE=ED=DC

a: Xét ΔABC có
BD là đường phân giác
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{AC}{BC}\left(1\right)\)
Xét ΔACB có
CE là đường phân giác
nên \(\dfrac{AE}{EB}=\dfrac{AC}{BC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AE}{EB}=\dfrac{AD}{DC}\)
hay ED//BC
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân

a: Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà BD=CE
nên BEDC là hình thang cân
b: Xét ΔEBD có \(\widehat{EBD}=\widehat{EDB}\left(=\widehat{DBC}\right)\)
nên ΔEBD cân tại E
Suy ra: ED=EB
mà EB=DC
nên BE=ED=DC
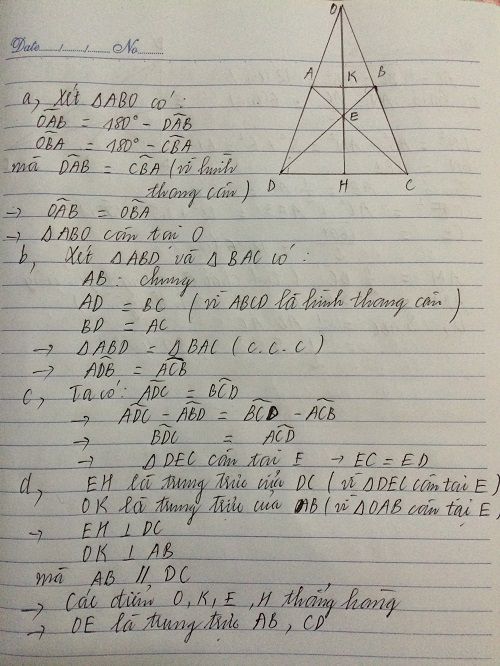
Lời giải:
Vì $D$ là trung điểm $AC, $E$ là trung điểm $AB$ nên $ED$ là đường trung bình ứng với cạnh $BC$ của tam giác $ABC$
$\Rightarrow ED\parallel BC$
$\Rightarrow BEDC$ là hình thang.
Mà 2 góc ở đáy $\widehat{B}=\widehat{C}$ (do tam giác $ABC$ cân tại $A$)
$\Rightarrow BEDC$ là hình thang cân.
Hình vẽ: