Nếu giảm 1 cạnh hình vuông 42m , giảm cạnh khác đi 6m thì được 1 hcn có chiều dài gấp 3 lần chiều rộng. Tính diện tích hv
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



gọi chiều dài,chiều rộng là:a,b
Theo bài
(a+4)(b+2)-ab=8
ab+4b+2a+8-ab=8
2a+4b+8=8
Nửa chu vi là:36:2=18
=>36+2b+8=8
44+2b=8
2b=8-44
2b=-36
b=-18
=>a là : 36
em nghĩ bài này chx chắc nên anh tham khảo

Bài 6:
Số đường thẳng là: \(4\cdot\dfrac{3}{2}=2\cdot3=6\left(đường\right)\)
Cứ 1 điểm sẽ tạo với 4 - 1 điểm còn lại 4 - 1 tia
Với 4 điểm ta sẽ tạo được số tia là:
(4 - 1) x 3 = 12 (tia)
Kết luận có 12 tia có gốc là một trong 4 điểm đã cho đó lần lượt là các tia:
EF; EG; EH; FE; FG; FH; GE; GF; GH; HE; HF; HG

Nửa chu vi mảnh vườn là:
36:2=18(m)
Gọi chiều dài mảnh vườn là x(m)
(ĐK: 0<x<18)
Chiều rộng mảnh vườn là 18-x(m)
Chiều dài khi tăng thêm 4m là x+4(m)
Chiều rộng khi giảm đi 2m là 18-x-2=16-x(m)
Diện tích tăng thêm 8m2 nên ta có:
(x+4)(16-x)-x(18-x)=8
=>\(16x-x^2+64-4x-18x+x^2=8\)
=>-6x=8-64=-56
=>\(x=\dfrac{56}{6}=\dfrac{28}{3}\left(nhận\right)\)
Vậy: Chiều dài mảnh vườn là 28/3(m)
Chiều rộng mảnh vườn là \(18-\dfrac{28}{3}=\dfrac{26}{3}\left(m\right)\)

(x+2)(y-3)
\(=x\cdot y-3\cdot x+2\cdot y-2\cdot3\)
=xy-3x+2y-6

a: \(1-\dfrac{1}{3}-\dfrac{1}{6}-\dfrac{1}{10}-\dfrac{1}{15}\)
\(=\dfrac{30-10-5-3-2}{30}\)
\(=\dfrac{10}{30}=\dfrac{1}{3}\)
b: \(\dfrac{8}{9}-\dfrac{1}{72}-\dfrac{1}{56}-\dfrac{1}{42}-\dfrac{1}{30}-\dfrac{1}{20}-\dfrac{1}{12}-\dfrac{1}{6}-\dfrac{1}{2}\)
\(=\dfrac{8}{9}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{8\cdot9}\right)\)
\(=\dfrac{8}{9}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\right)\)
\(=\dfrac{8}{9}-\left(1-\dfrac{1}{9}\right)=0\)
c: \(\left(-\dfrac{1}{2}\right)-\left(-\dfrac{3}{5}\right)+\left(-\dfrac{1}{9}\right)+\dfrac{1}{27}-\left(+\dfrac{7}{18}\right)+\dfrac{4}{35}-\left(-\dfrac{2}{7}\right)\)
\(=\dfrac{-1}{2}+\dfrac{3}{5}+\dfrac{-1}{9}+\dfrac{1}{27}-\dfrac{7}{18}+\dfrac{4}{35}+\dfrac{2}{7}\)
\(=\left(\dfrac{3}{5}+\dfrac{4}{35}+\dfrac{2}{7}\right)+\left(-\dfrac{1}{2}-\dfrac{1}{9}-\dfrac{7}{18}\right)+\dfrac{1}{27}\)
\(=\dfrac{21+4+10}{35}+\dfrac{-9-2-7}{18}+\dfrac{1}{27}\)
\(=\dfrac{35}{35}-\dfrac{18}{18}+\dfrac{1}{27}=\dfrac{1}{27}\)
d: \(\dfrac{3}{5}+\dfrac{3}{11}-\left(-\dfrac{3}{7}\right)+\left(\dfrac{2}{17}\right)-\dfrac{1}{35}-\dfrac{3}{4}+\left(-\dfrac{23}{44}\right)\)
\(=\left(\dfrac{3}{5}+\dfrac{3}{7}-\dfrac{1}{35}\right)+\left(\dfrac{3}{11}-\dfrac{3}{4}-\dfrac{23}{44}\right)+\dfrac{2}{17}\)
\(=\dfrac{21+15-1}{35}+\dfrac{12-33-23}{44}+\dfrac{2}{17}\)
\(=\dfrac{35}{35}-\dfrac{44}{44}+\dfrac{2}{17}=\dfrac{2}{17}\)

\(A=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{2019\cdot2021}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2019\cdot2021}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2019}-\dfrac{1}{2021}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{2021}\right)=\dfrac{1}{2}\cdot\dfrac{2020}{2021}=\dfrac{1010}{2021}< 1\)

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB~ΔOCD
b: Sửa đề: cắt BC tại N
Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)
=>\(OM\cdot AC=DC\cdot AO\)
c: Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BO}{BD}\left(2\right)\)
Ta có: ΔOAB~ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra OM=ON
=>O là trung điểm của MN

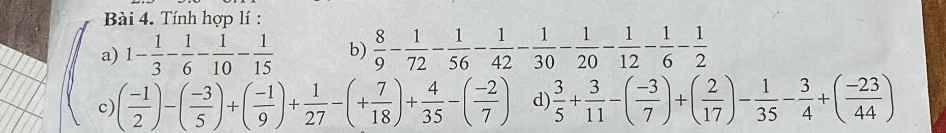

Ai nhanh mik tích