Cho 🔼ABC cân tại A. Trên cạnh AB lấy điểm D bất kì, trên tia dối của tia CA låy điểm E sao cho BD = CE. Từ D và E kẻ DM, EN cùng vuông góc với đường thẳng BC (M,N thuộc BC). Gọi I là giao điểm của DE với BC.
a, Chứng minh: DM = EN
b, Chứng minh: I là trung điểm của DE.
c, Khi điểm D di động trên cạnh AB. Chứng minh đường trung trực của đường thẳng DE luôn đi qua một định cố định.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{a-3}{a+3}=\dfrac{b-6}{b+6}\)
=>(a-3)(b+6)=(a+3)(b-6)
=>\(ab+6a-3b-18=ab-6a+3b-18\)
=>6a-3b=-6a+3b
=>12a=6b
=>\(\dfrac{a}{b}=\dfrac{6}{12}=\dfrac{1}{2}\)

Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{2x+3}{5}=\dfrac{y+11}{8}=\dfrac{6x+9}{15}=\dfrac{4y+44}{32}=\dfrac{6x+4y+53}{15+32}=\dfrac{2\left(3x+2y\right)+53}{47}=\dfrac{141}{47}=3\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2x+3}{5}=3\\\dfrac{y+11}{8}=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2x+3=15\\y+11=24\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=6\\y=13\end{matrix}\right.\)

\(\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}+\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}\)
\(=\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}\)
\(=\left(\dfrac{2}{3}+\dfrac{1}{3}\right)+\left(\dfrac{3}{4}+\dfrac{1}{4}\right)+\left(\dfrac{4}{5}+\dfrac{1}{5}\right)\)
\(=\dfrac{3}{3}+\dfrac{4}{4}+\dfrac{5}{5}\)
\(=1+1+1\)
\(=3\)
\(\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}+\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}=\)
Ta thấy: Ta có thể gạch được ở tử và mẫu của PS \(\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5}\), gạch hết các số giống nhau ta sẽ có \(\dfrac{2}{5}\)
Vậy: \(\dfrac{2}{5}+\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}\), ta thấy rằng mẫu số của tất cả các PS đều là 2 vậy ta quy đồng mẫu số hoặc rút gọn cho dễ tính
Ta rút gọn: \(\dfrac{2}{6}=\dfrac{1}{3},\dfrac{2}{8}=\dfrac{1}{4},\dfrac{2}{10}=\dfrac{1}{5}\)
= \(\dfrac{2}{5}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}\)
= \(\dfrac{2}{5}+\dfrac{1}{5}=\dfrac{3}{5}+\left(\dfrac{1}{4}+\dfrac{3}{4}\right)\)xin lỗi phần sau 3/5 là mình viết sai nhé!
= \(\dfrac{3}{5}+\left(\dfrac{1}{3}+\dfrac{1}{4}\right)\)
= \(\dfrac{3}{5}+\left(\dfrac{4}{12}+\dfrac{3}{12}\right)\)
= \(\dfrac{3}{5}+\dfrac{7}{12}\)
Vậy ta rút ra: Rút gọn phân số ko thể tính nhanh đc nên ta chuyển sang cách quy đồng

Lần thứ hai bán được số phần đàn gà là:
\(\dfrac{2}{7}+\dfrac{1}{14}=\dfrac{5}{14}\) (đàn gà)
Hai lần trại gà bán được số phần đàn gà là:
\(\dfrac{2}{7}+\dfrac{5}{14}=\dfrac{9}{14}\) (đàn gà)
ĐS: ...

\(6x^2+4xy-y^2\)
\(=6\left(x^2+\dfrac{2}{3}xy-\dfrac{1}{6}y^2\right)\)
\(=6\left(x^2+2\cdot x\cdot\dfrac{1}{3}y+\dfrac{1}{9}y^2-\dfrac{5}{18}y^2\right)\)
\(=6\left[\left(x+\dfrac{1}{3}y\right)^2-\left(\dfrac{y\sqrt{5}}{3\sqrt{2}}\right)^2\right]\)
\(=6\left(x+\dfrac{1}{3}y-\dfrac{y\sqrt{10}}{6}\right)\left(x+\dfrac{1}{3}y+\dfrac{y\sqrt{10}}{6}\right)\)
b: \(8x^2+3xy-4y^2\)
\(=8\left(x^2+\dfrac{3}{8}xy-\dfrac{1}{2}y^2\right)\)
\(=8\left(x^2+2\cdot x\cdot\dfrac{3}{16}y+\dfrac{9}{256}y^2-\dfrac{137}{256}y^2\right)\)
\(=8\left[\left(x+\dfrac{3}{16}y\right)^2-\left(\dfrac{y\sqrt{137}}{16}\right)^2\right]\)
\(=8\left(x+\dfrac{3}{16}y-\dfrac{y\sqrt{137}}{16}\right)\left(x+\dfrac{3}{16}y+\dfrac{y\sqrt{137}}{16}\right)\)

a) Chiều cao của bể là:
\(2,4:\dfrac{6}{5}=2\left(m\right)\)
Thể tích của bể là:
\(4,5\times2,4\times2=21,6\left(m^3\right)\)
Bể chứa được tối đa số lít nước là:
\(21,6\left(m^3\right)=21600\left(dm^3\right)=21600\left(l\right)\)
b) Thể tích nước có trong bể hiện tại là:
\(4,5\times2,4\times0,6=6,48\left(m^3\right)\)
Cần đổ thêm số mét khối nước nữa cho bể đầy là:
\(21,6-6,48=15,12\left(m^3\right)\)
ĐS: ...

\(2^x+4\cdot2^x=5\)
\(\Rightarrow2^x\cdot\left(1+4\right)=5\)
\(\Rightarrow2^x\cdot5=5\)
\(\Rightarrow2^x=\dfrac{5}{5}\)
\(\Rightarrow2^x=1\)
\(\Rightarrow2^x=2^0\)
\(\Rightarrow x=0\)
Vậy: `x=0`

\(B=\dfrac{39-\dfrac{6}{5}-\dfrac{3}{7}+\dfrac{3}{11}}{91-\dfrac{14}{5}-1+\dfrac{7}{11}}+\dfrac{\dfrac{5}{3}+\dfrac{15}{11}-3,5}{\dfrac{17}{51}-0,7+\dfrac{3}{11}}\)
\(=\dfrac{3}{7}\cdot\dfrac{\dfrac{7}{3}\cdot\left(39-\dfrac{6}{5}-\dfrac{3}{7}+\dfrac{3}{11}\right)}{91-\dfrac{14}{5}-1+\dfrac{7}{11}}+\dfrac{\dfrac{5}{3}+\dfrac{15}{11}-\dfrac{7}{2}}{\dfrac{1}{3}+\dfrac{3}{11}-\dfrac{7}{10}}\)
\(=\dfrac{3}{7}\cdot\dfrac{91-\dfrac{14}{5}-1+\dfrac{7}{11}}{91-\dfrac{14}{5}-1+\dfrac{7}{11}}+5\cdot\dfrac{\dfrac{1}{5}\cdot\left(\dfrac{5}{3}+\dfrac{15}{11}-\dfrac{7}{2}\right)}{\dfrac{1}{3}+\dfrac{3}{11}-\dfrac{7}{10}}\)
\(=\dfrac{3}{7}\cdot1+5\cdot\dfrac{\dfrac{1}{3}+\dfrac{3}{11}-\dfrac{7}{10}}{\dfrac{1}{3}+\dfrac{3}{11}-\dfrac{7}{10}}\)
\(=\dfrac{3}{7}+5\)
\(=\dfrac{38}{7}\)

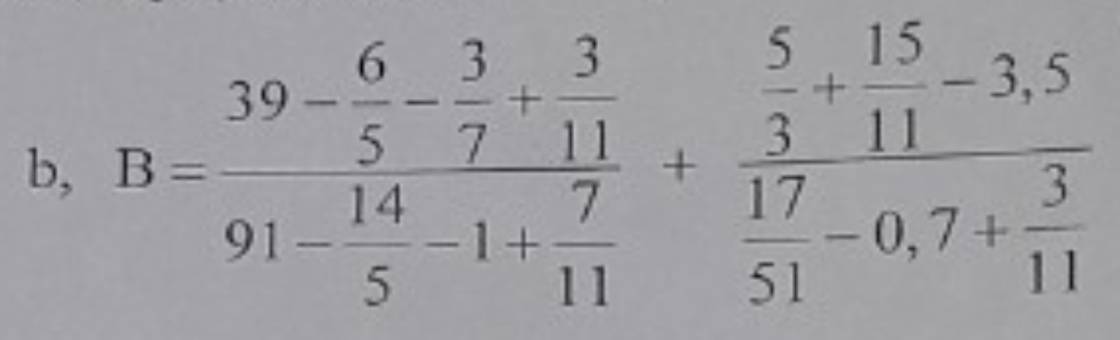
a: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{NCE}\)(hai góc đối đỉnh)
nên \(\widehat{ABC}=\widehat{NCE}\)
Xét ΔDMB vuông tại M và ΔENC vuông tại N có
DB=EC
\(\widehat{DBM}=\widehat{ECN}\)
Do đó: ΔDMB=ΔENC
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
=>\(\widehat{IDM}=\widehat{IEN}\)
Xét ΔIMD vuông tại M và ΔINE vuông tại N có
DM=EN
\(\widehat{MDI}=\widehat{NEI}\)
Do đó: ΔIMD=ΔINE
=>ID=IE
=>I là trung điểm của DE
bạn có thẻ vẽ hình cho mình không