A = \(\sqrt{3+2\sqrt{2}}\) - \(\sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\)

A = \(\sqrt{2+2\sqrt{2}+1}\) - \(\sqrt{\dfrac{\left(\sqrt{2}-1\right)\left(\sqrt{2}-1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)

A = \(\sqrt{\left(\sqrt{2}+1\right)^2}\) - \(\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{2-1}}\)

A = \(\sqrt{2}\) + 1 - \(\sqrt{2}\) + 1

A = 2

A = \(\dfrac{2+\sqrt{3}}{\sqrt{7-4\sqrt{3}}}\) - \(\dfrac{2-\sqrt{3}}{\sqrt{7+4\sqrt{3}}}\)

A = \(\dfrac{2+\sqrt{3}}{\sqrt{4-4\sqrt{3}+3}}\) - \(\dfrac{2-\sqrt{3}}{\sqrt{4+4\sqrt{3}+3}}\)

A = \(\dfrac{2+\sqrt{3}}{\sqrt{\left(2-\sqrt{3}\right)^2}}\) - \(\dfrac{2-\sqrt{3}}{\sqrt{\left(2+\sqrt{3}\right)^2}}\)

A = \(\dfrac{2+\sqrt{3}}{2-\sqrt{3}}\) - \(\dfrac{2-\sqrt{3}}{2+\sqrt{3}}\)

A = \(\dfrac{\left(2+\sqrt{3}\right)^2-\left(2-\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right).\left(2+\sqrt{3}\right)}\) 

A = \(\dfrac{\left(2+\sqrt{3}-2+\sqrt{3}\right)\left(2+\sqrt{3}+2-\sqrt{3}\right)}{4-3}\)

A = \(\dfrac{2\sqrt{3}.4}{1}\)

A = 8\(\sqrt{3}\)

\(y=x^8+\left(m-2\right)x^5-4\left(m^2-4\right)+1\)

Tập xác định \(D=ℝ\)

\(y'=8x^7+5\left(m-2\right)x^4\)

\(y''=56x^6+20\left(m-2\right)x^3\)

Để hàm số đạt cực tiểu tại \(x=0\)

\(\left\{{}\begin{matrix}y'\left(0\right)=0\\y''\left(0\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}0m=0\\0m>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\forall m\inℝ\\m>0\end{matrix}\right.\) \(\Leftrightarrow m>0\)

Vậy \(m>0\) hàm số trên đạt cực tiểu tại \(x=0\)

Với đề thi THPT quốc gia môn Toán, đây là một trong những câu khó. Không nhiều các bạn học sinh giải được đề toán trên. Đây là một hàm số bậc 8, hoàn toàn khác với những hàm số thông dụng được học trên lớp, để giải được bài này, các bạn cần phải sử dụng kiến thức từ định nghĩa và tính chất của cực trị hàm số bất kì. Ta có:

y" = 8x7 + 5(m - 2)x4 - 4(m2 - 4)x3 + 1

Hàm đạt cực tiểu tại x = 0 thì y"(x) = 0 và y"(x) đổi dấu từ âm sang dương khi x chạy qua điểm 0. Từ đó ta tương đương với số hạng chứa x có lũy thừa thấp nhất có hệ số khác 0 trong biểu thức y’ là lũy thừa bậc lẻ, hệ số dương.

Có nghĩa là :

–4(m2 - 4) > 0 và m - 2 = m² – 4 = 0

⇔ –2 Bài 2 - Mã đề 124 đề thi môn Toán THPT Quốc gia 2017

Dưới đây là hàm số y = f(x) được thể hiện trong bình với bảng biến thiên:

Tìm giá trị cực tiểu, cực đại của hàm số đã cho.

Bài giải:

Theo như bảng biến thiên các em học sinh nhận thấy được cực tiểu là 0 và giá trị cực đại của hàm số là 3.

Nhiều câu hỏi cho sẵn bảng biến thiên hay hình vẽ đồ thị hàm số sẽ xuất hiện trong đề thi. Chúng ta có thể vận dụng chính những dữ liệu này để có cho mình được đáp án đúng một cách nhanh chóng.

Đây nhé bro:))!

Số tổ là Ước của 48 = {1;2;3;4;6;8;12;16;24;48}

Theo đề bài có các cách chia tổ là 4 hoặc 6 tổ

a) \(A=\left\{34;124;128\right\}\)

b) \(B=\left\{315;483\right\}\)

c) \(C=\left\{315\right\}\)

a. \(A=\left\{34;124;128\right\}\)

b. \(B=\left\{315;483;\right\}\)

c. \(C=\left\{315\right\}\)

Bài 1 :

Phần trăm học sinh trung bình :

\(100\%-\left(60\%+30\%\right)=10\%=0,1\)

Tổng số học sinh là :

\(4:0,1=40\left(Hs\right)\)

Bài 2 :

Số phần trăm tiền lời và hạ giá là :

\(16\%+5\%=21\%\)

Số tiền vốn của chiếc cặp là :

\(45000:\left(100\%+21\%\right)\sim37190=37000\left(đồng\right)\)

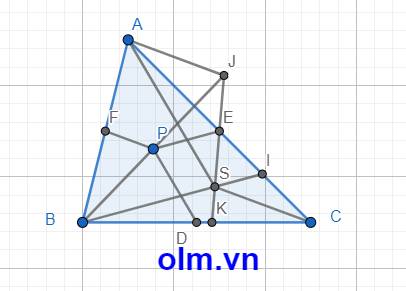
Gọi J là giao điểm của BP và KE; Xét \(\Delta\)BSJ có:

PE // BS; PE = \(\dfrac{1}{2}\) BS 

⇒ PF là đường trung bình của \(\Delta\)BSJ (vì đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy)

⇒ PJ = PB;  EJ = ES (1)

Xét \(\Delta\)ABJ có: AF = FB (gt); PJ = PB  theo (1)

⇒  PF là đường trung bình của \(\Delta\) ABJ (vì đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và song song với cạnh còn lại)

 ⇒ PF// AJ  (2) 

Xét tứ giác ASCJ ta có: E là giao điểm hai đường chéo

     AE = EC (gt)

    EJ = ES ( theo (1)

⇒ Tứ giác ASCJ là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.

⇒ CS // CJ (3)

Kết hợp (2) và(3) ta có:

     CS // PF ( vì trong cùng một mặt phẳng hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.)

  Kết luận: nếu BS = 2EP thì  CS // PF điều phải chứng minh

Chiểu cao của hình thang ABCD là: 12 \(\times\) 2 : 3 = 8 (cm)

Tổng độ dài hai đáy của hình thang là: 100 \(\times\) 2 : 8 = 25(cm)

Ta có sơ đồ:

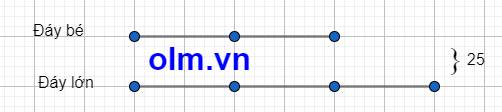
Theo sơ đồ ta có: Đáy bé: 25: ( 2+3) \(\times\) 2 = 10 (cm)

                              Đáy lớn là: 25 - 10 = 15 (cm)

                               Đáp số: Đáy bé 10 cm 

                                             Đáy lớn 15 cm 

\(\dfrac{3}{2}.x-\dfrac{2}{7}.x< x-\dfrac{7}{2}\ge18\)

\(\Rightarrow\left\{{}\begin{matrix}x-\dfrac{7}{2}>\dfrac{3}{2}.x-\dfrac{2}{7}.x\\x-\dfrac{7}{2}\ge18\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x-\dfrac{3}{2}.x+\dfrac{2}{7}.x>\dfrac{7}{2}\\x\ge18+\dfrac{7}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left(1-\dfrac{3}{2}+\dfrac{2}{7}\right).x>\dfrac{7}{2}\\x\ge\dfrac{36}{2}+\dfrac{7}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left(\dfrac{14}{14}-\dfrac{21}{14}+\dfrac{4}{14}\right).x>\dfrac{7}{2}\\x\ge\dfrac{43}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left(-\dfrac{3}{14}\right).x>\dfrac{7}{2}\\x\ge\dfrac{43}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x< \dfrac{7}{2}:\left(-\dfrac{3}{14}\right)\\x\ge\dfrac{43}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x< \dfrac{7}{2}.\left(-\dfrac{14}{3}\right)\\x\ge\dfrac{43}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x< -\dfrac{49}{3}\\x\ge\dfrac{43}{2}\end{matrix}\right.\) \(\Rightarrow x\in\varnothing\)

Bài toán này kiến thức vượt lớp 5 (dấu . là dấu nhân)

giiups tui nhanh nhanh

a) Ta có: x²\(\ge0,\forall x\) 

=> x² +3/4 \(\ge\dfrac{3}{4}\) , mọi x

Vậy min A = 3/4

Dấu "=" xảy ra <=> x =0

b) ( x- 3/2)² -0,4

Ta có ( x-3/2)² lớn hơn hoặc bằng 0, mọi x

=> ( x-3/2)² - 0,4 lớn hơn hoặc bằng 0 - 0;4 = -0,4

Vậy min B =-0,4

Dấu "=" xảy ra <=> x = 3/2

Chúc bạn học tốt !

bạn cho mik hỏi là min A nghĩa là sao vậy

= -5/9 - 4/9 + 8/15 +7/15

= -1 + 1

= 0

\(\dfrac{-5}{9}\)-\(\left(\dfrac{8}{15}+\dfrac{4}{9}\right)\)+\(\dfrac{7}{15}\)=\(\left(\dfrac{-5}{9}-\dfrac{4}{9}\right)\)-\(\left(\dfrac{8}{15}-\dfrac{7}{15}\right)\)=-1-1/15=-16/15.